K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
8 tháng 6 2021
Câu 1:
Biểu thức có nghĩa khi: $4-5x\geq 0\Leftrightarrow 4\geq 5x$
$\Leftrightarrow x\leq \frac{4}{5}$
Đáp án A.
Câu 2:
Căn bậc 2 số học của $13^2-12^2$ là $\sqrt{13^2-12^2}=\sqrt{25}=5$
Đáp án C
Câu 3: D (chắc mình không cần giải thích)
AH
Akai Haruma
Giáo viên
8 tháng 6 2021
Câu 4:
$\sqrt[3]{-125}=\sqrt[3]{(-5)^3}=-5$
Đáp án B.
Câu 5:
$\sqrt{x-2}-3=0$
$\sqrt{x-2}=3$
$x-2=9$
$x=11$
Đáp án D.
Câu 6:
Đường thẳng đi qua gốc tọa độ thì có dạng: $y=ax$ với $a\in\mathbb{R}$
ĐT này cắt $(d)$ nên: $a\neq -1$
Đáp án C.
MB
3
20 tháng 10 2021
Câu 12.
\(5\sqrt{a}+6\sqrt{\dfrac{a}{4}}-a\sqrt{\dfrac{4}{a}}+5\sqrt{\dfrac{4a}{25}}\)
\(=5\sqrt{a}+6\dfrac{\sqrt{a}}{2}-a\cdot\dfrac{2}{\sqrt{a}}+5\dfrac{2\sqrt{a}}{5}\)
\(=5\sqrt{a}+3\sqrt{a}-2\sqrt{a}+2\sqrt{a}\) (vì a>0)
\(=8\sqrt{a}\)
LN
2
1 tháng 11 2021
\(\sqrt{-x^2+2x-1}=\sqrt{-\left(x^2-2x+1\right)}=\sqrt{-\left(x-1\right)^2}\)
Do \(-\left(x-1\right)^2\le0\forall x\)
Nên căn thức chỉ xác định khi x=1
MB
2
6 tháng 11 2021
Áp dụng tslg trong tam giác DEF vuông tại D:
\(tanE=\dfrac{DF}{ED}=\dfrac{4}{3}\Rightarrow\widehat{E}\approx53^0\)
MH
28 tháng 9 2021
a) \(\sqrt{x-5}=3\)
\(x-5=9\)
\(x=14\)
b) Vì \(\sqrt{x-10}\) ≥0
⇒không có x thỏa mãn
c) \(\sqrt{2x-1}=\sqrt{7}\)
\(2x-1=7\)
\(2x=8\)
\(x=4\)
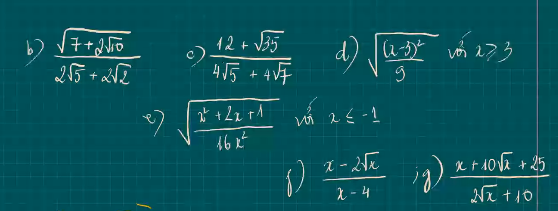
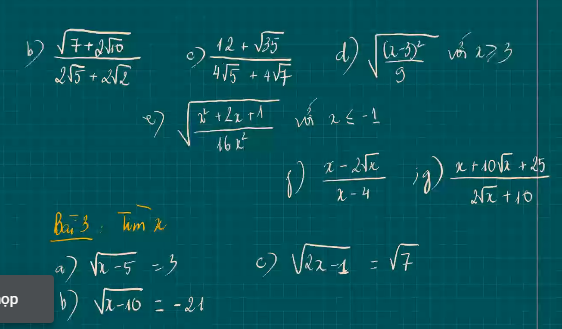
Thẳng thắng như thế này , em nên tự lực mình làm trước. Nếu như khó khăn, thắc mắc câu gì thì hãy lên đây hỏi. Mọi người không có quá nhiều thời gian để giải chi tiết tất cả trắc nghiệm cho em như tự luận được.