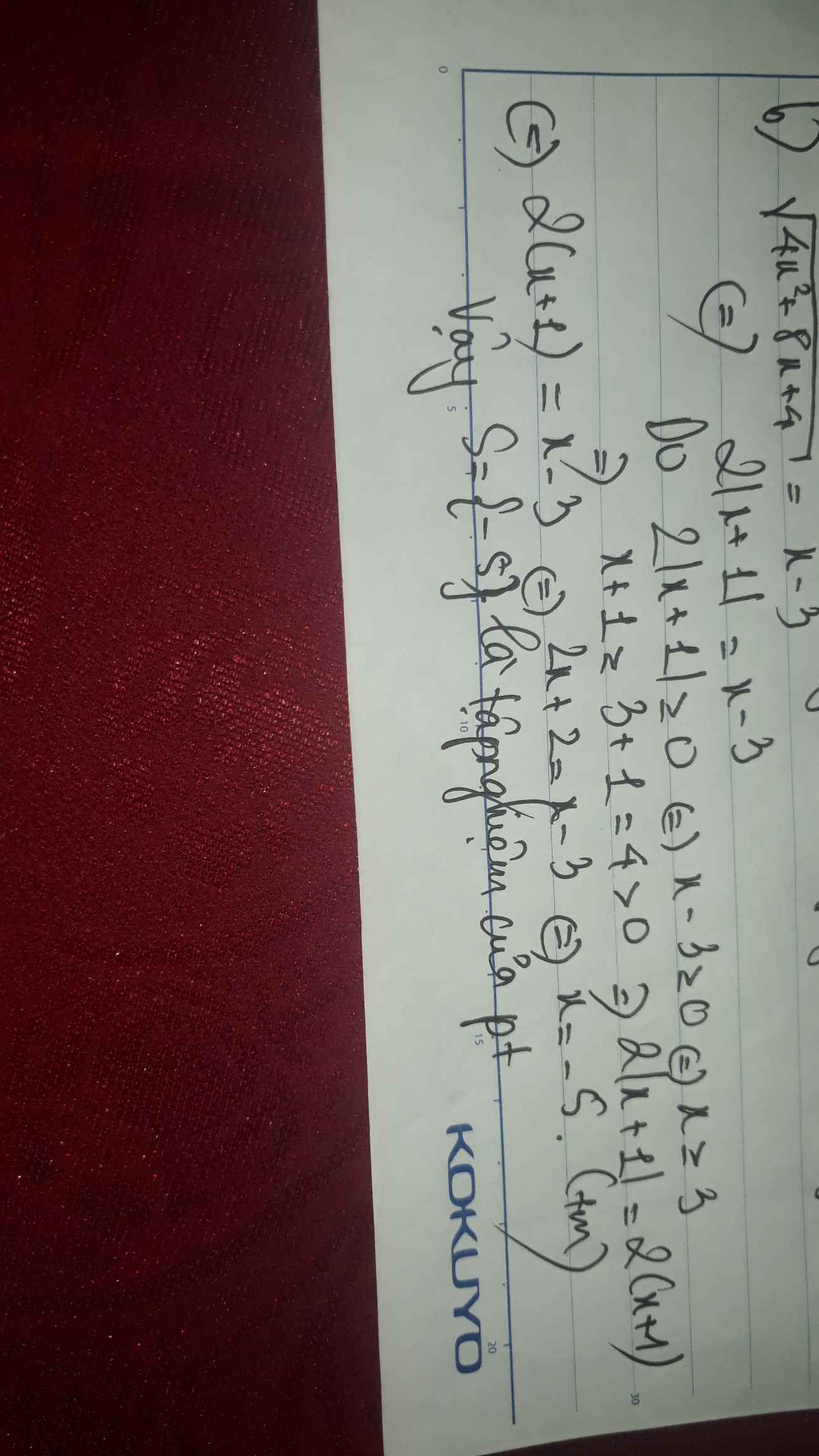K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KB
1
5 tháng 10 2019
PT \(\Leftrightarrow\sqrt{2\left(x+1\right)\left(x+3\right)}+\sqrt{\left(x-1\right)\left(x+1\right)}-2\left(x+1\right)=0\)
\(\Leftrightarrow\sqrt{x+1}\left(\sqrt{2\left(x+3\right)}+\sqrt{x-1}-2\sqrt{x+1}\right)=0\)
\(\Rightarrow\orbr{\begin{cases}\sqrt{x+1}=0\\\sqrt{2\left(x+3\right)}+\sqrt{x-1}-2\sqrt{x+1}=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=-1\\\sqrt{2\left(x+3\right)}+\sqrt{x-1}=2\sqrt{x+1}\end{cases}}\)
Xét \(\sqrt{2\left(x+3\right)}+\sqrt{x-1}=2\sqrt{x+1}\)
\(\Leftrightarrow2\left(x+3\right)+x-1+2\sqrt{2\left(x+3\right)\left(x-1\right)}=4\left(x+1\right)\)
\(\Leftrightarrow2\sqrt{2\left(x+3\right)\left(x-1\right)}=x-1\)
\(\Leftrightarrow8\left(x+3\right)\left(x-1\right)-\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(7x+25\right)=0\Rightarrow x=1\) ( t/m)
Vậy nghiệm của PT là : \(x=\pm1\)
Chúc bạn học tốt !!!
PG
1
24 tháng 3 2020
\(3\sqrt{8x^2+3}-8x=6\sqrt{2x^2-2x+1}-1\)
\(\Leftrightarrow3\left(\sqrt{8x^2+3}-2\sqrt{2x^2-2x+1}\right)-8x+1=0\)
\(\Leftrightarrow\frac{3\left(8x-1\right)}{\sqrt{8x^2+1}+2\sqrt{2x^2-2x+1}}-\left(8x-1\right)=0\)
\(\Leftrightarrow\left(8x-1\right)\left[\frac{3}{\sqrt{8x^2+3}+2\sqrt{2x^2-2x+1}}-1\right]=0\)
<=> 8x-1=0
<=> x=\(\frac{1}{8}\)
19 tháng 11 2019
Đặt \(\sqrt{2x^2-8x+12}=a>0\)thì được
\(2\left(x^2-4x-6\right)=2\sqrt{2x^2-8x+12}\)
\(\Leftrightarrow2x^2-8x-12=2\sqrt{2x^2-8x+12}\)
\(\Rightarrow a^2-2a-24=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=6\\a=-4\left(loai\right)\end{cases}}\)
\(\Rightarrow\sqrt{2x^2-8x+12}=6\)
\(\Leftrightarrow\orbr{\begin{cases}x=-2\\x=6\end{cases}}\)
ND
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 1 2022
ĐKXĐ: \(x\ge0\)
\(\sqrt{2x^2+8x+5}-4\sqrt{x}+\sqrt{2x^2-4x+5}-2\sqrt{x}=0\)
\(\Leftrightarrow\dfrac{2x^2-8x+5}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-8x+5}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)
\(\Leftrightarrow\left(2x^2-8x+5\right)\left(\dfrac{1}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{1}{\sqrt{2x^2-4x+5}+2\sqrt{x}}\right)=0\)
\(\Leftrightarrow2x^2-8x+5=0\)
\(\Leftrightarrow...\)
CH
Cô Hoàng Huyền
Admin
VIP
20 tháng 10 2017
a) ĐK: \(0\le x\le\frac{\sqrt{5}+1}{2}\)
\(\sqrt{1-\sqrt{x^2-x}}=\sqrt{x}-1\)
\(\Leftrightarrow1-\sqrt{x^2-x}=\left(\sqrt{x}-1\right)^2\left(x\ge1\right)\)
\(\Leftrightarrow1-\sqrt{x^2-x}=x-2\sqrt{x}+1\)
\(\Leftrightarrow\sqrt{x\left(x-1\right)}=2\sqrt{x}-x\)
\(\Leftrightarrow\sqrt{x\left(x-1\right)}=\sqrt{x}\left(2-\sqrt{x}\right)\)
\(\Leftrightarrow\sqrt{x}\left(\sqrt{x-1}+\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x}=0\\\sqrt{x-1}+\sqrt{x}-2=0\end{cases}}\)
TH1: x = 0 (Loại)
TH2: \(\sqrt{x-1}+\sqrt{x}-2=0\)
\(\Leftrightarrow\sqrt{x-1}=2-\sqrt{x}\)
\(\Leftrightarrow x-1=4-4\sqrt{x}+x\left(x\le4\right)\)
\(\Leftrightarrow4\sqrt{x}=5\Leftrightarrow\sqrt{x}=\frac{5}{4}\Leftrightarrow x=\frac{25}{16}\left(tm\right)\)
b) \(\sqrt{2x^2+8x+6}+\sqrt{x^2-1}=2x+2\)
ĐK: \(x\ge1\)
\(pt\Leftrightarrow\sqrt{\left(x+1\right)\left(2x+6\right)}+\sqrt{\left(x+1\right)\left(x-1\right)}=2\left(x+1\right)\)
\(\Leftrightarrow\sqrt{x+1}\left(\sqrt{2x+6}+\sqrt{x-1}-2\sqrt{x+1}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x+1}=0\\\sqrt{2x+6}+\sqrt{x-1}-2\sqrt{x+1}=0\end{cases}}\)
TH1: \(\sqrt{x+1}=0\Leftrightarrow x=-1\left(l\right)\)
TH2: \(\sqrt{2x+6}=2\sqrt{x+1}-\sqrt{x-1}\)
\(\Leftrightarrow2x+6=4\left(x+1\right)+\left(x-1\right)-4\sqrt{x^2-1}\)
\(\Leftrightarrow2x+6=5x+3-4\sqrt{x^2-1}\)
\(\Leftrightarrow4\sqrt{x^2-1}=3x-3\Leftrightarrow16\left(x^2-1\right)=9x^2-18x+9\left(x\ge1\right)\)
\(\Leftrightarrow7x^2+18x-25=0\Leftrightarrow\orbr{\begin{cases}x=1\left(tm\right)\\x=-\frac{25}{7}\left(l\right)\end{cases}}\)
19 tháng 10 2017
dk tu xd \(\sqrt{2x^2+8x+6}\) \(+\sqrt{x^2-1}=2x+2\)
\(\Leftrightarrow\sqrt{2\left(x+1\right)\left(x+3\right)}-\sqrt{\left(x-1\right)\left(x+1\right)}-2\left(x+1\right)=0\)
\(\Leftrightarrow\sqrt{x+1}\left(2\sqrt{x+3}-\sqrt{x-1}-2\sqrt{x+1}\right)=0\)
đến đây bn tự giải nhé
A
0
TK
1
TN
8 tháng 6 2017
Đk:\(x\ge\frac{4}{5}\)
\(pt\Leftrightarrow2x-1+\sqrt{5x-4}-\sqrt{8x^2+2x-6}=0\)
\(\Leftrightarrow\left(\sqrt{5x-4}-\left(2x-1\right)\right)-\left(\sqrt{8x^2+2x-6}-\left(4x-2\right)\right)=0\)
\(\Leftrightarrow\frac{\left(5x-4\right)-\left(2x-1\right)^2}{\sqrt{5x-4}+2x-1}-\frac{\left(8x^2+2x-6\right)-\left(4x-2\right)^2}{\sqrt{8x^2+2x-6}+4x-2}=0\)
\(\Leftrightarrow\frac{-\left(x-1\right)\left(4x-5\right)}{\sqrt{5x-4}+2x-1}-\frac{-2\left(x-1\right)\left(4x-5\right)}{\sqrt{8x^2+2x-6}+4x-2}=0\)
\(\Leftrightarrow-\left(x-1\right)\left(4x-5\right)\left(\frac{1}{\sqrt{5x-4}+2x-1}-\frac{2}{\sqrt{8x^2+2x-6}+4x-2}\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\4x-5=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=1\\x=\frac{5}{4}\end{cases}}\) (thỏa mãn)
