
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 46:
a, \(x+y=2=>\left(x+y\right)^2=4\)\(=>x^2+y^2+2xy=4=>10+2xy=4\)
\(=>xy=\dfrac{4-10}{2}=-3\)
\(x^3+y^3=x^3+3x^2y+3xy^2+y^3-3xy\left(x+y\right)\)
\(=\left(x+y\right)^3\)\(-3xy\left(x+y\right)=2^3-3.\left(-3\right).2=26\)
\(b,\) \(x+y=a=>x^2+2xy+y^2=a^2\)
\(=>xy=\dfrac{a^2-b}{2}\)
có: \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=a^3-3\left(\dfrac{a^2-b}{2}\right)a\)
\(=a^3-\dfrac{3a^3-3ab}{2}\)

a) Gọi n = a2 + b2
Suy ra 2n = 2a2 + 2b2 = a2 + 2ab + b2 + a2 - 2ab + b2
= (a + b)2 + (a - b)2
b) theo đề bài ta có: 2n = a2 + b2
=> n= a2/2 + b2/2 => (a2/4 + 2.a/2.b/2 + b2/4) + (a2/4 + 2a/2.b/2 + b2/4
= (a + b)2/2 + (a - b)2/2
c) n2 = (a2 + b2)2 = a4 + 2a2.b2 + b4 = a4 - 2a2.b2 + b4 + 4a2.b2
= (a2 - b2)2 + (2ab)2
d) m.n = (a2 + b2)(c2 + d2) = a2.c2 + a2. d2 + b2.c2 + b2.d22
= (a2.c2 + 2a2.b2.c2.d2 + b2.d2) + (a2.d2 - 2a2.b2.c2.d2 + b2.c2)
= (ac +ab)2 + (ad + bc)2

Gọi chiều rộng hình chữ nhật là x>0 (m)
Chiều dài hình chữ nhật: \(x+1\) (m)
Diện tích ban đầu: \(x\left(x+1\right)\)
Chiều dài sau khi thay đổi: \(\dfrac{5}{4}\left(x+1\right)\)
Diện tích lúc sau: \(\dfrac{5}{4}x\left(x+1\right)\)
Ta có pt:
\(\dfrac{5}{4}x\left(x+1\right)-x\left(x+1\right)=3\)
\(\Leftrightarrow x\left(x+1\right)=12\Leftrightarrow x^2+x-12=0\Rightarrow\left[{}\begin{matrix}x=3\\x=-4< 0\left(loại\right)\end{matrix}\right.\)
Diện tích hcn ban đầu: \(3.\left(3+1\right)=12\left(m^2\right)\)


Bài 5:
a: Ta có: \(x^2-8x+17\)
\(=x^2-8x+16+1\)
\(=\left(x-4\right)^2+1>0\forall x\)
b: Ta có: \(4x^2-12x+13\)
\(=4x^2-12x+9+4\)
\(=\left(2x-3\right)^2+4>0\forall x\)
c: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)


Bài 1:
a) Xét tứ giác BHCN có
BH//CN(gt)
BN//CH(gt)
Do đó: BHCN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Ta có: BHCN là hình bình hành(cmt)
nên Hai đường chéo BC và HN cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà M là trung điểm của BC(gt)
nên M là trung điểm của HN
hay H,M,N thẳng hàng(đpcm)

\(3x^2-2x+5=0\)
\(\Leftrightarrow2x^2+x^2-2x+1+4=0\)
\(\Leftrightarrow2x^2+\left(x-1\right)^2=-4\)
Phương trình vô nghiệm.
Sai đề phải là 3x2-2x-5=0
Ta có:3x2-2x-5=0
<=> 3x2+3x-5x-5=0
<=> 3x(x+1)-5(x+1)=0
<=> (x+1)(3x-5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{5}{3}\end{matrix}\right.\)

Ta có: \(\Delta ABC\sim\Delta MNP\)
\(\Rightarrow\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}=\dfrac{1}{2}\)
mà AB = 4 cm, BC = 6 cm, AC = 5 cm. Thay vào, ta lại có:
\(\Rightarrow\dfrac{4}{MN}=\dfrac{5}{MP}=\dfrac{6}{NP}=\dfrac{1}{2}\)
\(\Rightarrow MN=\dfrac{2.4}{1}=8\left(cm\right)\)
\(\Rightarrow MP=5.2=10\left(cm\right)\)
\(\Rightarrow NP=6.2=12\left(cm\right)\)





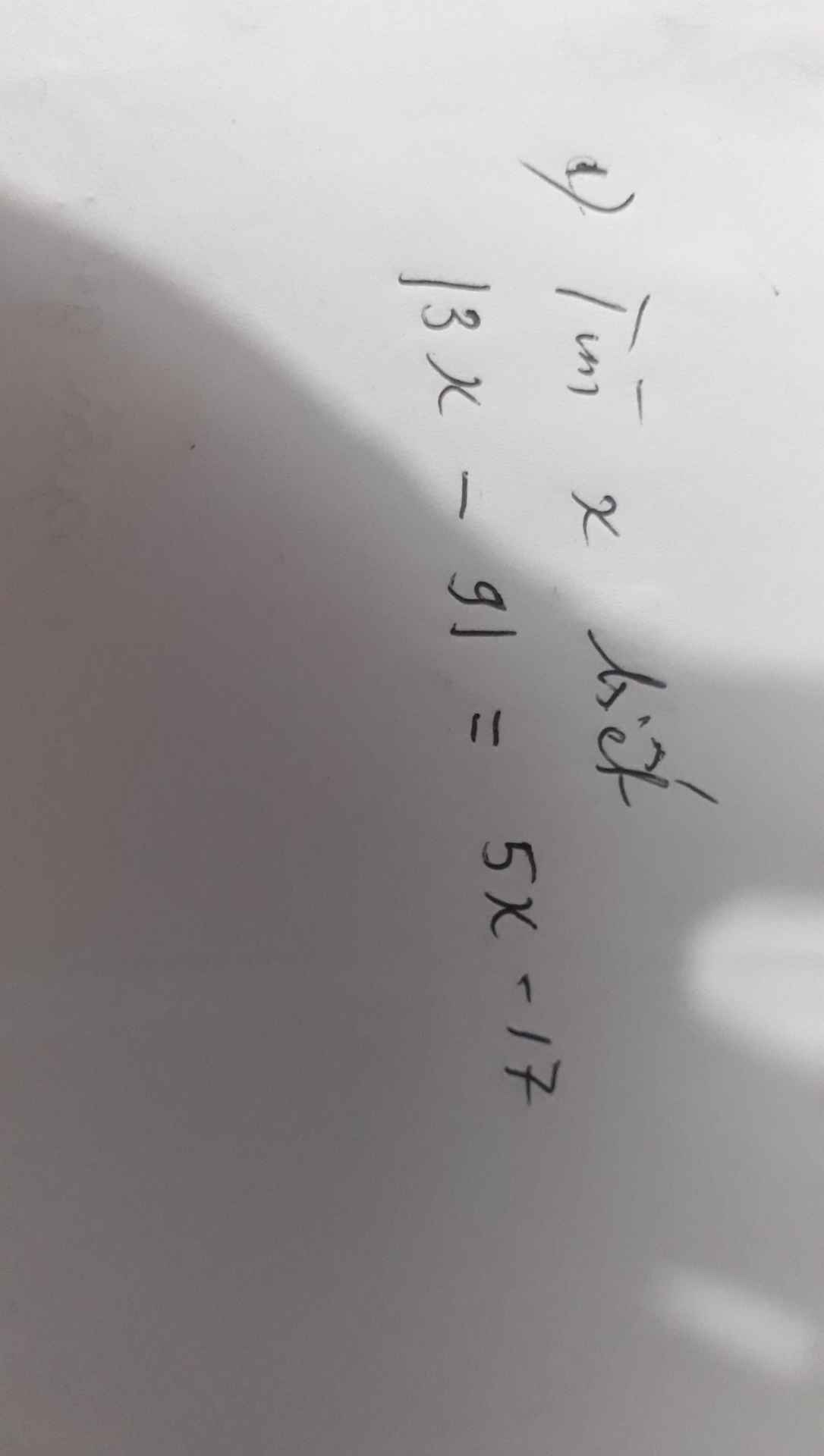


 giải chi tiết hộ mik với ạ.
giải chi tiết hộ mik với ạ.
dùng hệ số ổn ko nhỉ
Thực hiện phép chia, ta được: \(12x^3-7x^2-14x+14=\left(3x^2+2x-1\right)\left(4x-5\right)+9\)
Vậy để \(2x^3-7x^2-14x+14⋮4x-5\) thì \(9⋮4x-5\)
\(\Rightarrow4x-5\inƯ\left(9\right)=\left\{-9;-1;1;9\right\}\\ 4x-5=-9\Rightarrow x=-1\\ 4x-5=9\Rightarrow x=\frac{3}{2}\\ 4x-5=1\Rightarrow x=\frac{3}{2}\\ 4x-5=-1\Rightarrow x=1\)
Vậy giá trị x<0 để \(2x^3-7x^2-14x+14⋮4x-5\) là x=-1