
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Điều kiện xác định :
\(\left\{{}\begin{matrix}2x-2\ne0\\x-1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\ne2\\x\ne1\end{matrix}\right.\)
\(\Leftrightarrow x\ne1\)
\(\dfrac{2x+1}{2x-2}=\dfrac{2}{x-1}\)
\(\Leftrightarrow\dfrac{2x+1}{2x-2}-\dfrac{2}{x-1}=0\)
\(\Leftrightarrow\dfrac{2x+1}{2\left(x-1\right)}-\dfrac{2}{x-1}=0\)
\(\Leftrightarrow\dfrac{2x+1-2.2}{2\left(x-1\right)}=0\)
\(\Leftrightarrow2x+1-4=0\)
\(\Leftrightarrow2x-3=0\)
\(\Leftrightarrow x=\dfrac{3}{2}\left(tmdk\right)\)
Vậy \(S=\left\{\dfrac{3}{2}\right\}\)

\(\left(x-1\right)^3+x^3+\left(x+1\right)^3=\left(x+2\right)^3\)
\(\Leftrightarrow x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1-x^3-6x^2-12x-8=0\)
\(\Leftrightarrow2x^3-6x^2-6x-8=0\)
\(\Leftrightarrow2.\left(x^3-3x^2-3x-4\right)=0\)
\(\Leftrightarrow x^3-4x^2+x^2-4x+x-4=0\)
\(\Leftrightarrow x^2.\left(x-4\right)+x.\left(x-4\right)+\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right).\left(x^2+x+1\right)=0\)
Mà \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
\(\Rightarrow x-4=0\Leftrightarrow x=4\)

a) \(\Leftrightarrow x^2+10x+25-x^2+8x-15=-8\\ \Leftrightarrow18x=-18\\ \Leftrightarrow x=-1\)
b) \(\Leftrightarrow\left(2x+1\right)^2-3\left(2x+1\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(2x+1-3\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(2x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)

\(\dfrac{1}{a}-\dfrac{a-4}{4a}=6\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\dfrac{4-\left(a-4\right)}{4a}=\dfrac{24a}{4a}\)
\(\Leftrightarrow4-\left(a-4\right)=24a\)
\(\Leftrightarrow4-a+4=24a\)
\(\Leftrightarrow8=25a\)
\(\Leftrightarrow a=\dfrac{8}{25}\left(tm\right)\)
Vậy \(S=\left\{\dfrac{8}{25}\right\}\)

\(\Leftrightarrow2x^2+10x-x^2+6x-9=x^2+6\)
=>16x-9=6
=>16x=15
hay x=15/16
\(PT\Leftrightarrow2x^2+10x-x^2+6x-9-x^2-6=0.\)
\(\Leftrightarrow16x-15=0.\\ \Leftrightarrow x=\dfrac{15}{16}.\)

Ta có:
(2 - 3x)(x + 8) = (3x - 2)(3 - 5x)
⇔ (2 - 3x)(x + 8) - (3x - 2)(3 - 5x) = 0
⇔ (2 - 3x)(x + 8) + (2 - 3x)(3 - 5x) = 0
⇔ (2 - 3x)(x + 8 + 3 - 5x) = 0
⇔ (2 - 3x)(11 - 4x) = 0
⇔ 2 - 3x = 0 hay 11 - 4x = 0
⇔ 2 = 3x hay 11 = 4x
⇔ x = \(\dfrac{2}{3}\) hay x = \(\dfrac{11}{4}\)
Vậy tập nghiệm của pt S = \(\left\{\dfrac{2}{3};\dfrac{11}{4}\right\}\)
<=> (2-3x ) (x+8) + (2-3x ) (3-5x)=0
<=> (2-3x ) ( x+8 + 3-5x ) =0
<=> (2-3x ) ( 11 - 4x ) = 0
=> 2-3x =0 hoặc 11-4x =0
3x = 2 4x =11
x = 2/3 x = 11/4

Ác MỘng Sai rồi kìa vì phải phân ra 2 trường hợp
Hoặc dương.dương=dương>0
âm.âm=dương>0
x^2 -4x +3 >=0 => (x-1)(x-3) >=0 => Hoặc cả hai điều x - 1 > = 0 và x-3 >=0 => x>= 1 và x> = 3
x - 1<= 0 và x - 3 <= 0 => x<= 1 và x<= 3
Tóm lại x>=3 hoặc x<=3

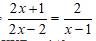


\(3x^2-2x+5=0\)
\(\Leftrightarrow2x^2+x^2-2x+1+4=0\)
\(\Leftrightarrow2x^2+\left(x-1\right)^2=-4\)
Phương trình vô nghiệm.
Sai đề phải là 3x2-2x-5=0
Ta có:3x2-2x-5=0
<=> 3x2+3x-5x-5=0
<=> 3x(x+1)-5(x+1)=0
<=> (x+1)(3x-5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{5}{3}\end{matrix}\right.\)