K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 7 2021
Em tách nhỏ ra rồi hỏi nhe!! VD như 1 bài hỏi 1 lần á
24 tháng 7 2021
3) Ta có: \(\dfrac{\sqrt{10}+\sqrt{15}}{\sqrt{8}+\sqrt{12}}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{2}+\sqrt{3}\right)}{2\left(\sqrt{2}+\sqrt{3}\right)}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{2\sqrt{5}-3\sqrt{5}}{4}\)
\(=\dfrac{-\sqrt{5}}{4}\)
LO
0
24 tháng 7 2021
1) Ta có: \(\dfrac{1}{\sqrt{3}-1}+\dfrac{1}{4+2\sqrt{3}}-\dfrac{2}{\sqrt{3}}-\dfrac{3}{2}\)
\(=\dfrac{\sqrt{3}+1}{2}+\dfrac{2-\sqrt{3}}{2}-\dfrac{2\sqrt{3}}{3}-\dfrac{3}{2}\)
\(=\dfrac{\sqrt{3}+1+2-\sqrt{3}-3}{2}-\dfrac{2\sqrt{3}}{3}\)
\(=-\dfrac{2\sqrt{3}}{3}\)
24 tháng 7 2021
3) Ta có: \(\dfrac{\sqrt{10}+\sqrt{15}}{\sqrt{8}+\sqrt{12}}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{2}+\sqrt{3}\right)}{2\left(\sqrt{2}+\sqrt{3}\right)}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{2\sqrt{5}-3\sqrt{5}}{4}\)
\(=\dfrac{-\sqrt{5}}{4}\)
PN
15 tháng 10 2017
Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125
Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*)
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**)
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0
=> AB^2 = 5605. Vì AB > 0 => AB = 75
AC = 4/3 x AC => AC = 100
Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC.
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có:
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80
15 tháng 10 2017
ti le 3 canh la 3/4/5 (dinh li pytago)
2 canh goc vuong lan luot la
125 : 5 x 4 = 100
125 : 5 x 3 = 75
5 tháng 8 2021
22,
1, Đặt √(3-√5) = A
=> √2A=√(6-2√5)
=> √2A=√(5-2√5+1)
=> √2A=|√5 -1|
=> A=\(\dfrac{\sqrt{5}-1}{\text{√2}}\)
=> A= \(\dfrac{\sqrt{10}-\sqrt{2}}{2}\)
2, Đặt √(7+3√5) = B
=> √2B=√(14+6√5)
=> √2B=√(9+2√45+5)
=> √2B=|3+√5|
=> B= \(\dfrac{3+\sqrt{5}}{\sqrt{2}}\)
=> B= \(\dfrac{3\sqrt{2}+\sqrt{10}}{2}\)
3,
Đặt √(9+√17) - √(9-√17) -\(\sqrt{2}\)=C
=> √2C=√(18+2√17) - √(18-2√17) -\(2\)
=> √2C=√(17+2√17+1) - √(17-2√17+1) -\(2\)
=> √2C=√17+1- √17+1 -\(2\)
=> √2C=0
=> C=0
26,
|3-2x|=2\(\sqrt{5}\)
TH1: 3-2x ≥ 0 ⇔ x≤\(\dfrac{-3}{2}\)
3-2x=2\(\sqrt{5}\)
-2x=2\(\sqrt{5}\) -3
x=\(\dfrac{3-2\sqrt{5}}{2}\) (KTMĐK)
TH2: 3-2x < 0 ⇔ x>\(\dfrac{-3}{2}\)
3-2x=-2\(\sqrt{5}\)
-2x=-2√5 -3
x=\(\dfrac{3+2\sqrt{5}}{2}\) (TMĐK)
Vậy x=\(\dfrac{3+2\sqrt{5}}{2}\)
6 tháng 8 2021
2, \(\sqrt{x^2}\)=12 ⇔ |x|=12 ⇔ x=12, -12
3, \(\sqrt{x^2-2x+1}\)=7
⇔ |x-1|=7
TH1: x-1≥0 ⇔ x≥1
x-1=7 ⇔ x=8 (TMĐK)
TH2: x-1<0 ⇔ x<1
x-1=-7 ⇔ x=-6 (TMĐK)
Vậy x=8, -6
4, \(\sqrt{\left(x-1\right)^2}\)=x+3
⇔ |x-1|=x+3
TH1: x-1≥0 ⇔ x≥1
x-1=x+3 ⇔ 0x=4 (KTM)
TH2: x-1<0 ⇔ x<1
x-1=-x-3 ⇔ 2x=-2 ⇔x=-1 (TMĐK)
Vậy x=-1
TH
1
G
6 tháng 4 2022
Ta có 1ml = 1cm3
Vậy thể tích của lọ đựng dung dịch đó là 100 cm3
Diện tích trong của đáy lọ là:
Ta có: V = S đáy * h => S đáy = V : h = 100 : 12.5 = 8 (cm2)
9 tháng 9 2021
a: Ta có: \(A=\dfrac{2x-3\sqrt{x}-14}{x-7\sqrt{x}+12}-\dfrac{\sqrt{x}+4}{\sqrt{x}-3}-\dfrac{\sqrt{x}-1}{\sqrt{x}-4}\)
\(=\dfrac{2x-3\sqrt{x}-14-x+16-x+4\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}\)
Ta có: \(B=\dfrac{x-2\sqrt{x}+1}{x-4\sqrt{x}+3}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}\)
b: Ta có: M=A:B
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\)
\(=\dfrac{1}{\sqrt{x}-4}\)
NN
1 tháng 11 2020
\(\sqrt{x^2+x-1}+\sqrt{x-x^2+1}=x^2-x+2\)
\(ĐKXĐ:\hept{\begin{cases}\sqrt{x^2+x-1}\ge0\\\sqrt{x-x^2+1}\ge0\end{cases}}\)
Vì \(\sqrt{x^2+x-1}\ge0\)
\(\Rightarrow\)Áp dụng bđt Cô-si ta có: \(1+\left(x^2+x-1\right)\ge2\sqrt{x^2+x-1}\)(1)
Tương tự ta có: \(1+\left(x-x^2+1\right)\ge2\sqrt{x-x^2+1}\)(2)
Cộng (1) và (2) ta có:
\(1+\left(x^2+x-1\right)+1+\left(x-x^2+1\right)\ge2\sqrt{x^2+x-1}+2\sqrt{x-x^2+1}\)
\(\Leftrightarrow1+x^2+x-1+1+x-x^2+1\ge2.\left(\sqrt{x^2+x-1}+\sqrt{x-x^2+1}\right)\)
\(\Leftrightarrow2+2x\ge2\left(\sqrt{x^2+x-1}+\sqrt{x-x^2+1}\right)\)
\(\Leftrightarrow1+x\ge\sqrt{x^2+x-1}+\sqrt{x-x^2+1}\)
\(\Leftrightarrow1+x\ge x^2-x+2\)
\(\Leftrightarrow x^2-x+2-1-x\le0\)
\(\Leftrightarrow x^2-2x+1\le0\)
\(\Leftrightarrow\left(x-1\right)^2\le0\)(3)
Vì \(\left(x-1\right)^2\ge0\forall x\)(4)
Từ (3) và (4) \(\Rightarrow\left(x-1\right)^2=0\)\(\Leftrightarrow x-1=0\)\(\Leftrightarrow x=1\)
Thay \(x=1\)vào ĐKXĐ ta thấy \(x=1\) thỏa mãn ĐKXĐ
Vậy \(x=1\)
PN
1 tháng 11 2020
\(\sqrt{x+x-1}+\sqrt{x-x^2+1}=x\left(x-1\right)+2\left(đk:...\ge x\ge\frac{1}{2}\right)\)( giải bpt này ra x-x2+1>=0 là tìm đc số trong dấu ...)
\(< =>\sqrt{x+x-1}-1+\sqrt{x-x^2+1}-1=x\left(x-1\right)\)
\(< =>\frac{2x-2}{\sqrt{x+x-1}+1}+\frac{x-x^2}{\sqrt{x-x^2+1}+1}=x\left(x-1\right)\)
\(< =>\frac{2\left(x-1\right)}{\sqrt{x+x-1}+1}+\frac{x\left(x-1\right)}{-\sqrt{x-x^2+1}-1}-x\left(x-1\right)=0\)
\(< =>\left(x-1\right)\left(\frac{2}{\sqrt{x+x-1}+1}+\frac{x}{-\sqrt{x-x^2+1}-1}-x\right)=0\)
\(< =>x=1\)( bạn đánh giá phần trong ngoặc to = đk ban đầu nhé )
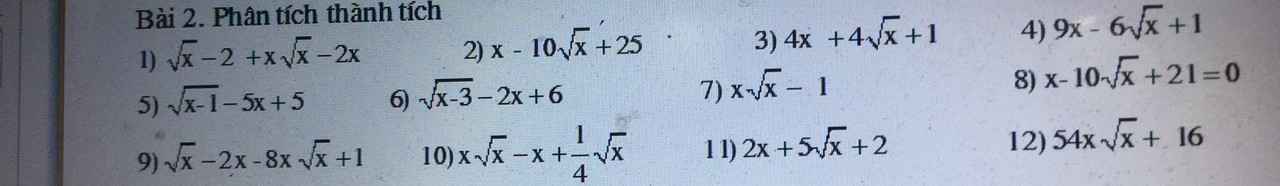
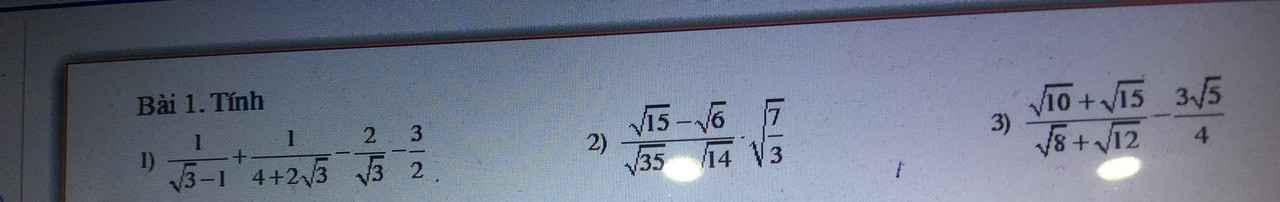
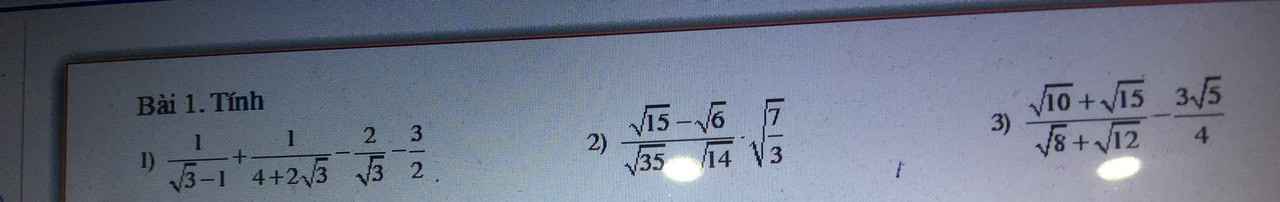
1.
\(\sqrt{x}-2+x\sqrt{x}-2x=(\sqrt{x}-2)+(x\sqrt{x}-2x)=(\sqrt{x}-2)+x(\sqrt{x}-2)\)
\(=(\sqrt{x}-2)(1+x)\)
2.
\(x-10\sqrt{x}+25=(\sqrt{x})^2-2.5.\sqrt{x}+5^2=(\sqrt{x}-5)^2\)
3.
\(4x+4\sqrt{x}+1=(2\sqrt{x})^2+2.2\sqrt{x}+1=(2\sqrt{x}+1)^2\)
4.
\(9x-6\sqrt{x}+1=(3\sqrt{x})^2-2.3\sqrt{x}+1=(3\sqrt{x}-1)^2\)
5.
\(\sqrt{x-1}-5x+5=\sqrt{x-1}-5(x-1)=\sqrt{x-1}(1-5\sqrt{x-1})\)
6.
\(\sqrt{x-3}-2x+6=\sqrt{x-3}-2(x-3)=\sqrt{x-3}(1-2\sqrt{x-3})\)
7.
\(x\sqrt{x}-1=(\sqrt{x})^3-1^3=(\sqrt{x}-1)(x+\sqrt{x}+1)\)
8.
\(x-10\sqrt{x}+21=x-3\sqrt{x}-(7\sqrt{x}-21)\)
\(=\sqrt{x}(\sqrt{x}-3)-7(\sqrt{x}-3)=(\sqrt{x}-7)(\sqrt{x}-3)\)