K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 8 2021
A= -x+\(4\sqrt{x}\)+5
A= -x+\(4\sqrt{x}\)-4+9
A= -(x-\(4\sqrt{x}\)+4)+9
A=-(\(\sqrt{x}\)-2)2 +9 ≤9
Dấu "=" xẩy ra khi -(\(\sqrt{x}\)-2)=0
=> x=4
Vậy Max A=9 khi x=4
17 tháng 8 2021
B=15-x+6\(\sqrt{x}\)
B= -x+6\(\sqrt{x}\)-9+24
B=-(\(\sqrt{x}\)-3)2+24
Dấu "=" xẫy ra khi x=9
Vậy Max B = 24 khi x= 9
20 tháng 10 2021
Bài 2:
\(\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{x}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=x-\sqrt{x}+1\)
HA
0
23 tháng 7 2021
Em tách nhỏ ra rồi hỏi nhe!! VD như 1 bài hỏi 1 lần á
24 tháng 7 2021
3) Ta có: \(\dfrac{\sqrt{10}+\sqrt{15}}{\sqrt{8}+\sqrt{12}}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{2}+\sqrt{3}\right)}{2\left(\sqrt{2}+\sqrt{3}\right)}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{2\sqrt{5}-3\sqrt{5}}{4}\)
\(=\dfrac{-\sqrt{5}}{4}\)
T
1
24 tháng 7 2021
1) Ta có: \(\dfrac{1}{\sqrt{3}-1}+\dfrac{1}{4+2\sqrt{3}}-\dfrac{2}{\sqrt{3}}-\dfrac{3}{2}\)
\(=\dfrac{\sqrt{3}+1}{2}+\dfrac{2-\sqrt{3}}{2}-\dfrac{2\sqrt{3}}{3}-\dfrac{3}{2}\)
\(=\dfrac{\sqrt{3}+1+2-\sqrt{3}-3}{2}-\dfrac{2\sqrt{3}}{3}\)
\(=-\dfrac{2\sqrt{3}}{3}\)
24 tháng 7 2021
3) Ta có: \(\dfrac{\sqrt{10}+\sqrt{15}}{\sqrt{8}+\sqrt{12}}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{2}+\sqrt{3}\right)}{2\left(\sqrt{2}+\sqrt{3}\right)}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{2\sqrt{5}-3\sqrt{5}}{4}\)
\(=\dfrac{-\sqrt{5}}{4}\)
3 tháng 7 2021
1) \(A=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{x\sqrt{x}-1}:\dfrac{\sqrt{x}-1}{5}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{5}{\sqrt{x}-1}\) \(=\dfrac{5}{x+\sqrt{x}+1}\)
2) Ta thấy \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>1\forall x\)
\(\Rightarrow A< 5\)
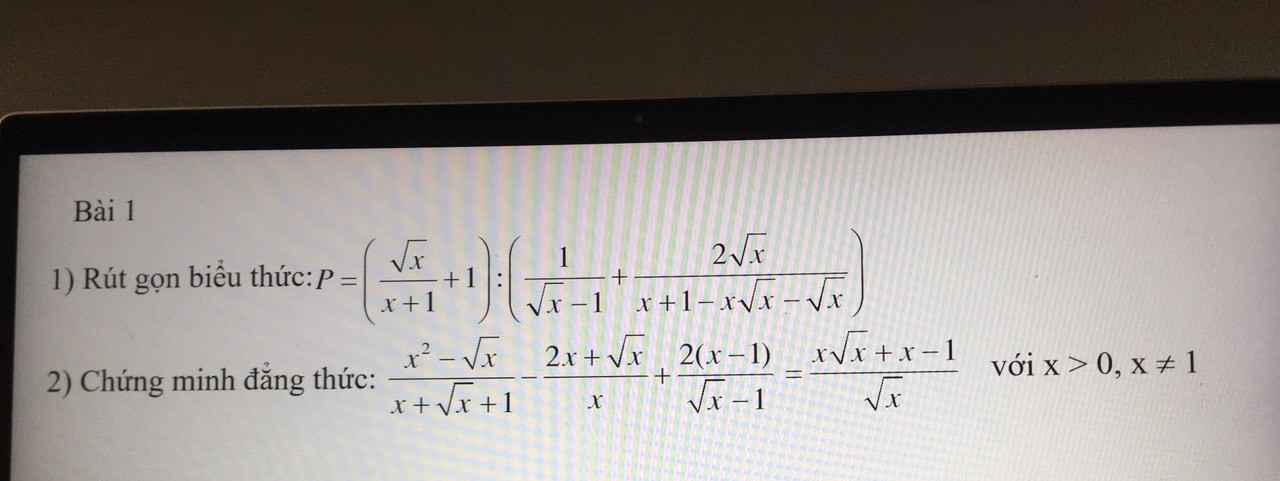
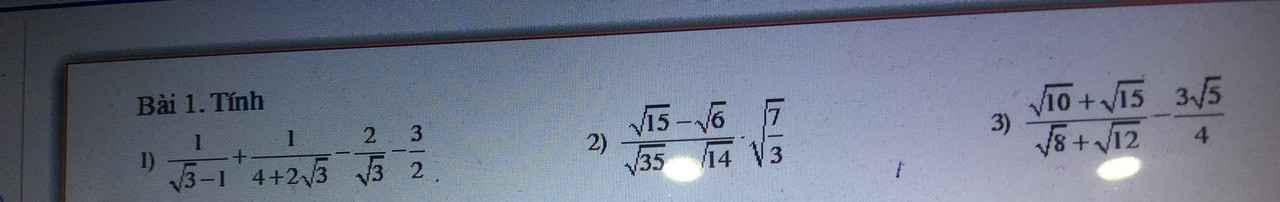
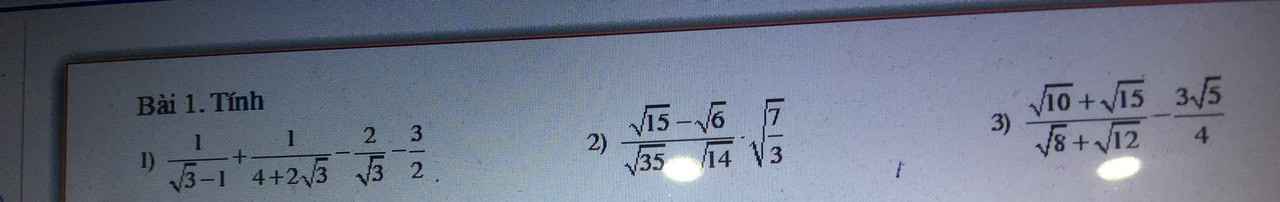
a: Ta có: \(A=\dfrac{2x-3\sqrt{x}-14}{x-7\sqrt{x}+12}-\dfrac{\sqrt{x}+4}{\sqrt{x}-3}-\dfrac{\sqrt{x}-1}{\sqrt{x}-4}\)
\(=\dfrac{2x-3\sqrt{x}-14-x+16-x+4\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}\)
Ta có: \(B=\dfrac{x-2\sqrt{x}+1}{x-4\sqrt{x}+3}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}\)
b: Ta có: M=A:B
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\)
\(=\dfrac{1}{\sqrt{x}-4}\)