K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AN
2
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
LH
1
AH
Akai Haruma
Giáo viên
6 tháng 7 2017
Lời giải:
Từ điều kiện $M$ nằm trên cạnh $BC$ và \(MC=2MB\) suy ra \(\overrightarrow{MC}=2\overrightarrow {BM}\)
Gọi \(M=(a,b,c)\Rightarrow (-3-a,6-b,4-c)=2(a,b-3,c-1)\)
\(\left\{\begin{matrix} -3-a=2a\\ 6-b=2(b-3)\\ 4-c=2(c-1)\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=-1\\ b=4\\ c=2\end{matrix}\right.\)
Do đó \(MA=\sqrt{29}\)
Vậy không có đáp án nào đúng
HN
14 tháng 3 2022
Anh (chị) vui lòng kiểm tra điều kiện của xA và xB giúp em ạ!
AN
2
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 8 2021
Từ đồ thị ta thấy \(f'\left(x\right)>0\) trên các khoảng \(\left(-1;1\right)\) và \(\left(3;+\infty\right)\)
\(f'\left(x\right)< 0\) trên \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)
\(\Rightarrow\) Hàm nghịch biến trên (1;3)
PT
25 tháng 5 2016
bạn tải về rồi zoom lên ý, vì đây là tớ chụp ảnh nên ảnh nhỏ
mong bạn tải về zoom lên hướng dẫn tớ với
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 6 2021
Ủa 2 kết quả giống nhau mà? Có sai chỗ nào đâu bạn?
TT
27 tháng 6 2021
Làm sao để biết nó bằng nhau vậy ạ..Mình calc x mà nó khác nhau
NT
3
E
19 tháng 1 2022
log2 2 vế ta có: x = 2log2x
<=> x - 2.log2x = 0
Đặt f(x) = x - 2.log2x
f'(x) = 1 - \(\dfrac{2}{x.ln2}\)
Dễ thấy f'(x) có 1 nghiệm duy nhất. Nên theo định lý Rolle: pt f(x) = 0 có tối đa 2 nghiệm phân biệt
Mà x = 2 và x = 4 là 2 nghiệm của pt f(x) = 0
Nên pt có tập nghiệm S = {2; 4}
Thi trắc nghiệm mà vẫn giải tự luận à
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
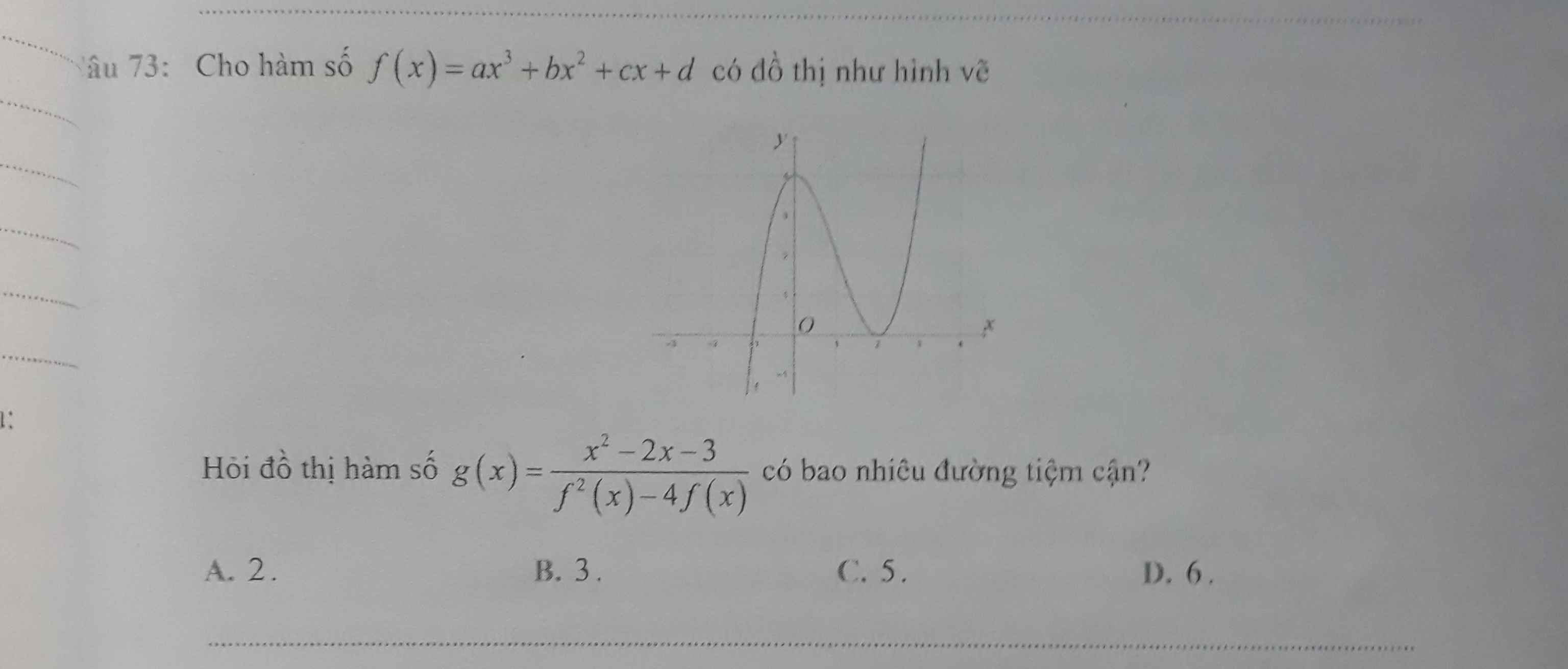
có cái gì đâu