


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1. \(\left(2x^2-3x+1\right)+\left(3x^2+2x-1\right)\)
\(=2x^2-3x+1+3x^2+2x-1\)
\(=\left(2x^2+3x^2\right)-\left(3x-2x\right)+\left(1-1\right)\)
\(=5x^2-x\)
2. \(\left(4x^3-2x^2+3x\right)-\left(2x^3+3x^2-4x\right)\)
\(=4x^3-2x^2+3x-2x^3-3x^2+4x\)
\(=\left(4x^3-2x^3\right)-\left(2x^2+3x^2\right)+\left(3x+4x\right)\)
\(=2x^3-5x^2+7x\)
3. \(\left(x^2-5x+6\right)+\left(-3x^2+2x-1\right)\)
\(=x^2-5x+6-3x^2+2x-1\)
\(=\left(x^2-3x^2\right)-\left(5x-2x\right)+\left(6-1\right)\)
\(=-2x^2-3x+5\)
4. \(\left(2x^3+5x^2-3x+1\right)-\left(x^3-2x^2+x-1\right)\)
\(=2x^3+5x^2-3x+1-x^3+2x^2-x+1\)
\(=\left(2x^3-x^3\right)+\left(5x^2+2x^2\right)-\left(3x+x\right)+\left(1+1\right)\)
\(=x^3+7x^2-4x+2\)
5. \(\left(3x^2+2x-4\right)+\left(4x^2-x+5\right)\)
\(=3x^2+2x-4+4x^2-x+5\)
\(=\left(3x^2+4x^2\right)+\left(2x-x\right)-\left(4-5\right)\)
\(=7x^2+x+1\)
6. \(\left(x^3-2x^2+5x-1\right)-\left(2x^3+3x^2-4x+2\right)\)
\(=x^3-2x^2+5x-1-2x^3-3x^2+4x-2\)
\(=\left(x^3-2x^3\right)-\left(2x^2+3x^2\right)+\left(5x+4x\right)-\left(1+2\right)\)
\(=-x^3-5x^2+9x-3\)

`a,`
`P(x)=x^2-5+x^4-4x^3-x^6`
`P(x)= -x^6+x^4-4x^3+x^2-5`
`Q(x)=2x^5-x^4+x^2-x^3+x-1`
`Q(x)=2x^5-x^4-x^3+x^2+x-1`
`b,`
`P(x)+Q(x)=(-x^6+x^4-4x^3+x^2-5)+(2x^5-x^4-x^3+x^2+x-1)`
`= -x^6+x^4-4x^3+x^2-5+2x^5-x^4-x^3+x^2+x-1`
`= -x^6+2x^5+(x^4-x^4)+(-4x^3-x^3)+(x^2+x^2)+x+(-5-1)`
`= -x^6+2x^5-5x^3+2x^2+x-6`
`c,`
`P(x)-Q(x)=(-x^6+x^4-4x^3+x^2-5)-(2x^5-x^4-x^3+x^2+x-1)`
`= -x^6+x^4-4x^3+x^2-5-2x^5+x^4+x^3-x^2-x+1`
`= -x^6-2x^5+(x^4+x^4)+(-4x^3+x^3)+(x^2-x^2)+x+(-5+1)`
`= -x^6-2x^5+2x^4-3x^3+x-4`
Ote.
Phần trừ đa thức một biến, bạn phải chú ý trước có dấu trừ, bạn ngoặc vào nhé! Còn trước dấu ngoặc có dấu trừ, đổi dấu. Khi gộp và rút gọn các đa thức cùng bậc, chú ý trước dấu ngoặc nên để dấu cộng, khi gộp vào phải đưa nguyên dấu của hạng tử, không được tự tiện đổi. Những cái này là phải nhớ nhé!

\(\Rightarrow2^{3n-n}=16=2^4\Rightarrow2n=4\Rightarrow n=2\)

x + y + xy = 2
x + y(x + 1) = 2
x + 1 + y(x + 1) = 3
(x + 1)(y + 1) = 3
=> x + 1 và y + 1 thuộc ước của 3
Ư(3) = { - 3; - 1; 1; 3 }
Ta có bảng sau :
| x + 1 | - 3 | - 1 | 3 | 1 |
| y + 1 | - 1 | - 3 | 1 | 3 |
| x | - 4 | - 2 | 2 | 0 |
| y | - 2 | - 4 | 0 | 2 |
Vậy ( x;y ) = { ( -4;-2 );( -2;-4 );( 2;0 );( 0;2 ) }

1. Định nghĩa hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :
2. Các trường hợp bằng nhau của tam giác vuông
• Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh )
• Cạnh góc vuông và góc nhọn kề cạnh đó
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc )
• Cạnh huyền – góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc)
• Cạnh huyền – cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
1. Định nghĩa hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :
2. Các trường hợp bằng nhau của tam giác
a. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Xét 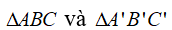
AB = A’B’
AC = A’C’
BC = B’C’
thì
b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau
c. Trường hợp bằng nhau thứ ba của hai tam giác: góc – cạnh – góc
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
tik cho mình nha mình đc câu1 nè

a/\(F\left(x\right)=-4x^2+7-6x+5x^3\)
\(=5x^3-4x^2-6x+7\)
\(G\left(x\right)=4x^2+9x-2x^4+4x^3-12\)
\(=-2x^4+4x^3+4x^2+9x-12\)
b/\(F\left(x\right)+G\left(x\right)=\left(5x^3-4x^2-6x+7\right)+\left(-2x^4+4x^3+4x^2+9x-12\right)\)
\(=5x^3-4x^2-6x+7-2x^4+4x^3+4x^2+9x-12\)
\(=\left(5x^3+4x^3\right)-\left(4x^2-4x^2\right)+\left(-6x+9x\right)-2x^4-\left(-7+12\right)\)
\(=9x^3-0+3x-2x^4-5\)
\(=9x^3+3x-2x^4-5\)

2:
a: \(A\left(x\right)=3x^3-2x^2-5x+3\)
\(B\left(x\right)=5x^3+x^2+2x-1\)
b: A(x)+B(x)=8x^3-x^2-3x+2
c: A(x)-B(x)
=3x^3-2x^2-5x+3-5x^3-x^2-2x+1
=-2x^3-3x^2-7x+4

a: \(=2x^2-3x+1+3x^2+2x-1=5x^2-x\)
b: \(=4x^3-2x^2+3x-2x^3-3x^2+4x=2x^3-5x^2+7x\)
c: \(=x^2-5x+6-3x^2+2x-1=-2x^2-3x+5\)
d: \(=2x^3+5x^2-3x+1-x^3+2x^2-x+1\)
\(=x^3+7x^2-4x+2\)
e: \(=3x^2+2x-4+4x^2-x+5=7x^2+x+1\)
f: \(=x^3-2x^2+5x-1-2x^3-3x^2+4x-2=-x^3-5x^2+9x-3\)
g: \(=4x^4-3x^3+x^2+2x-1+2x^3-4x^2+3x-1\)
\(=4x^4-x^3-3x^2+5x-2\)

a: \(=2x^2-3x+1+3x^2+2x-1=5x^2-x\)
b: \(=4x^3-2x^2+3x-2x^3-3x^2+4x=2x^3-5x^2+7x\)
c: \(=x^2-5x+6-3x^2+2x-1=-2x^2-3x+5\)
d: \(=2x^3+5x^2-3x+1-x^3+2x^2-x+1\)
\(=x^3+7x^2-4x+2\)
e: \(=3x^2+2x-4+4x^2-x+5=7x^2+x+1\)
f: \(=x^3-2x^2+5x-1-2x^3-3x^2+4x-2=-x^3-5x^2+9x-3\)
g: \(=4x^4-3x^3+x^2+2x-1+2x^3-4x^2+3x-1\)
\(=4x^4-x^3-3x^2+5x-2\)