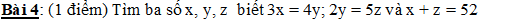K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 9 2021
ta có ∠1=70o(hai góc đối đỉnh)
hai đường thẳng a và b cùng cắt c tạo thành 30o+150o=180omà hai góc ở vị trí trong cùng phía
=>a//b(dấu hiệu)
=>∠1=∠2(hai góc đồng vị) ta lại có: ∠1=70o(cmt)=>∠2=70o
mà ∠2=∠3(hai góc đối đỉnh)=>∠3=70o
bài hơi khó hiểu(tại bạn không ghi rõ tên góc đó)
4 tháng 3 2022
Bài 4:
Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó:ABCD là hình bình hành
Suy ra: AD//BC
Xét tứ giác AEBC có
M là trung điểm của AB
M là trung điểm của EC
Do đó: AEBC là hình bình hành
Suy ra: AE//CB
mà AD//BC
và AE,AD có điểm chung là A
nên E,A,D thẳng hàng
1 tháng 8 2016
Theo đầu bài ta có:
\(\frac{x+1}{2}=\frac{y+3}{4}=\frac{z+5}{6}\)
\(\Rightarrow\frac{2\cdot\left(x+1\right)}{2\cdot2}=\frac{3\cdot\left(y+3\right)}{3\cdot4}=\frac{4\cdot\left(z+5\right)}{4\cdot6}\)
\(\Rightarrow\frac{2x+2}{4}=\frac{3y+9}{12}=\frac{4z+20}{24}\)
\(=\frac{\left(2x+2\right)+\left(3y+9\right)+\left(4z+20\right)}{4+12+24}\)
\(=\frac{\left(2x+3y+4z\right)+\left(2+9+20\right)}{4+12+24}\)
\(=\frac{9+31}{40}=1\)
\(\Rightarrow\hept{\begin{cases}x=1\cdot2-1=1\\y=1\cdot4-3=1\\z=1\cdot6-5=1\end{cases}}\)
10 tháng 11 2021
a)ABE = 180 độ - 35 độ = 145 độ
b) Vì DBC + BCy = 180 độ
=>Cy // DE
mà DE // Ax
=>Ax//Cy
BA
1
23 tháng 9 2021
Ta có: \(3x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}\)
\(2y=5z\Rightarrow\dfrac{y}{5}=\dfrac{z}{2}\Rightarrow\dfrac{y}{15}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{6}=\dfrac{x+z}{20+6}=\dfrac{52}{26}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=20.2=40\\y=15.2=30\\z=6.2=12\end{matrix}\right.\)
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
VN
11 tháng 1 2023
a)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y+z}{3+5+6}=\dfrac{98}{14}=7\)
\(+)\)\(\dfrac{x}{3}=7\Rightarrow x=7\times3=21\)
\(+)\)\(\dfrac{y}{5}=7\Rightarrow y=7\times5=35\)
\(+)\)\(\dfrac{z}{6}=7\Rightarrow z=7\times6=42\)
Vậy \(x=21;y=35;z=42\)
b)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{2}=\dfrac{x+y-z}{4+5-2}=\dfrac{21}{7}=3\)
\(+)\)\(\dfrac{x}{4}=3\Rightarrow x=3\times4=12\)
\(+)\)\(\dfrac{y}{5}=3\Rightarrow y=3\times5=15\)
\(+)\)\(\dfrac{z}{2}=3\Rightarrow z=3\times2=6\)
Vậy \(x=12;y=15;z=6\)
c)
Ta có :
\(x:y:z=5:\left(-6\right):7\) và \(x-y-z=16\)
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}\) và \(x-y-z=16\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}=\dfrac{x-y-z}{5-\left(-6\right)-7}=\dfrac{16}{4}=4\)
\(+)\)\(\dfrac{x}{5}=4\Rightarrow x=4\times5=20\)
\(+)\)\(\dfrac{y}{-6}=4\Rightarrow y=4\times\left(-6\right)=-24\)
\(+)\)\(\dfrac{z}{7}=4\Rightarrow z=4\times7=28\)
Vậy \(x=20;y=-24;z=28\)
d)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+z}{2+4}=\dfrac{18}{6}=3\)
\(+)\)\(\dfrac{x}{2}=3\Rightarrow x=3\times2=6\)
\(+)\)\(\dfrac{y}{3}=3\Rightarrow y=3\times3=9\)
\(+)\)\(\dfrac{z}{4}=3\Rightarrow z=3\times4=12\)
Vậy \(x=6;y=9;z=12\)
e)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{7}=\dfrac{x-y}{5-6}=\dfrac{36}{-1}=-36\)
\(+)\)\(\dfrac{x}{5}=-36\Rightarrow x=-36\times5=-180\)
\(+)\)\(\dfrac{y}{6}=-36\Rightarrow y=-36\times6=-216\)
\(+)\)\(\dfrac{z}{7}=-36\Rightarrow z=-36\times7=-252\)
Vậy \(x=-180;y=-216;z=-252\)
11 tháng 1 2023
a: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y+z}{3+5+6}=\dfrac{98}{14}=7\)
=>x=21; y=35; z=42
b: x/4=y/5=z/2 và x+y-z=21
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{2}=\dfrac{x+y-z}{4+5-2}=\dfrac{21}{7}=3\)
=>x=12; y=15; z=6
c: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}=\dfrac{x-y-z}{5+6-7}=\dfrac{16}{4}=4\)
=>x=20; y=-24; z=28
d: Áp dụng tính chất của DTSBN, ta được:
x/2=y/3=z/4=(x+z)/(2+4)=18/6=3
=>x=6; y=9; z=12
