Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,\text{PT hoành độ giao điểm: }3x-1=x+2\\ \Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow y=\dfrac{7}{2}\Leftrightarrow A\left(\dfrac{3}{2};\dfrac{7}{2}\right)\\ \text{Vậy }A\left(\dfrac{3}{2};\dfrac{7}{2}\right)\text{ là giao 2 đths}\\ c,\left(D_2\right)\text{//}\left(D\right);B\left(1;0\right)\in\left(D_2\right)\Leftrightarrow\left\{{}\begin{matrix}a+b=0\\a=3;b\ne-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-3\end{matrix}\right.\\ \Leftrightarrow\left(D_2\right):y=3x-3\)

e: Ta có: \(\sqrt{x^2+3x+1}=\sqrt{x+1}\)\(\)
\(\Leftrightarrow x^2+3x=x\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=-2\left(loại\right)\end{matrix}\right.\)


\(\Leftrightarrow2\sqrt{x-4}=5\left(x\ge4\right)\\ \Leftrightarrow\sqrt{x-4}=\dfrac{5}{2}\\ \Leftrightarrow x-4=\dfrac{25}{4}\\ \Leftrightarrow x=\dfrac{41}{4}\left(tm\right)\)

Lời giải :
\(x^8+x+1\)
\(=x^8-x^5+x^5-x^2+x^2+x+1\)
\(=x^5\left(x^3-1\right)+x^2\left(x^3-1\right)+\left(x^2+x+1\right)\)
\(=x^5\left(x-1\right)\left(x^2+x+1\right)+x^2\left(x-1\right)\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^6-x^5+x^3-x^2+1\right)\)


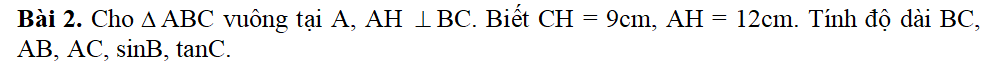

 mn gấp quá có ai giúp em vớiiii
mn gấp quá có ai giúp em vớiiii