
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(-1\le x\le4\)
\(\Leftrightarrow\left(x-3\right)\sqrt{1+x}-\left(x-3\right)+x-x\sqrt{4-x}=2x^2-6x\)
\(\Leftrightarrow\left(x-3\right)\left(\sqrt{1+x}-1\right)+x\left(1-\sqrt{4-x}\right)=2x^2-6x\)
\(\Leftrightarrow\dfrac{x\left(x-3\right)}{\sqrt{1+x}+1}+\dfrac{x\left(x-3\right)}{1+\sqrt{4-x}}=2\left(x^2-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x=0\Rightarrow x=...\\\dfrac{1}{\sqrt{1+x}+1}+\dfrac{1}{1+\sqrt{4-x}}=2\left(1\right)\end{matrix}\right.\)
Xét (1), do \(VT< \dfrac{1}{1}+\dfrac{1}{1}=2\Rightarrow VT< VP\Rightarrow\left(1\right)\) vô nghiệm
Vậy ...

Đường thẳng \(\Delta:\left\{{}\begin{matrix}x=1+4t\\y=2-3t\end{matrix}\right.\) đi qua điểm \(A\left(1;2\right)\) và có VTCP \(\overrightarrow{u}=\left(4;-3\right)\)
\(\Rightarrow\overrightarrow{n}=\left(3;4\right)\) là VTPT của đường thẳng
\(\Rightarrow\) PT tổng quát: \(3\left(x-1\right)+4\left(y-2\right)=0\Leftrightarrow3x+4y-11=0\)
\(\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|3.1+4.\left(-1\right)-11\right|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}\)


b) \(\dfrac{3\pi}{2}< \alpha< 2\pi\)\(\Rightarrow cos\alpha>0;sin\alpha< 0\)
Có \(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\)\(\Rightarrow cos\alpha=\dfrac{4}{5}\)
\(sin\alpha=-\sqrt{1-cos^2\alpha}=-\dfrac{3}{5}\)
\(sin\left(\alpha-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\left(sin\alpha-cos\alpha\right)=\dfrac{\sqrt{2}}{2}\left(-\dfrac{3}{5}-\dfrac{4}{5}\right)=-\dfrac{7\sqrt{2}}{10}\)
Bài 2:
a) Gọi đt d vuông góc với đường thẳng \(\Delta\)có dạng: \(d:-4x+3y+c=0\)
\(A\in\left(d\right)\Rightarrow-4+3+c=0\Leftrightarrow c=1\)
Vậy \(d:-4x+3y+1=0\)
b) Gọi pt đường tròn (C) tâm A có dạng \(\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=R^2\)
Vì (C) tiếp xúc với \(\Delta\)
\(\Rightarrow\)\(R=d_{\left(A;\Delta\right)}=\dfrac{\left|3+4+5\right|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}\)
\(\Rightarrow\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=\dfrac{144}{25}\)
Vậy...


ĐK: \(x\ge0\)
Dễ thấy \(1-\sqrt{2\left(x^2-x+1\right)}\le1-\sqrt{2}< 0\)
Khi đó bất phương trình tương đương:
\(x-\sqrt{x}\le1-\sqrt{2\left(x^2-x+1\right)}\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(x+\dfrac{1}{x}-1\right)}\le0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2+2}\le0\)
\(\Leftrightarrow t-1+\sqrt{2t^2+2}\le0\)


a: Tham số là 2m-1
Ẩn số là x
b: Tham số là n
Ẩn số là x

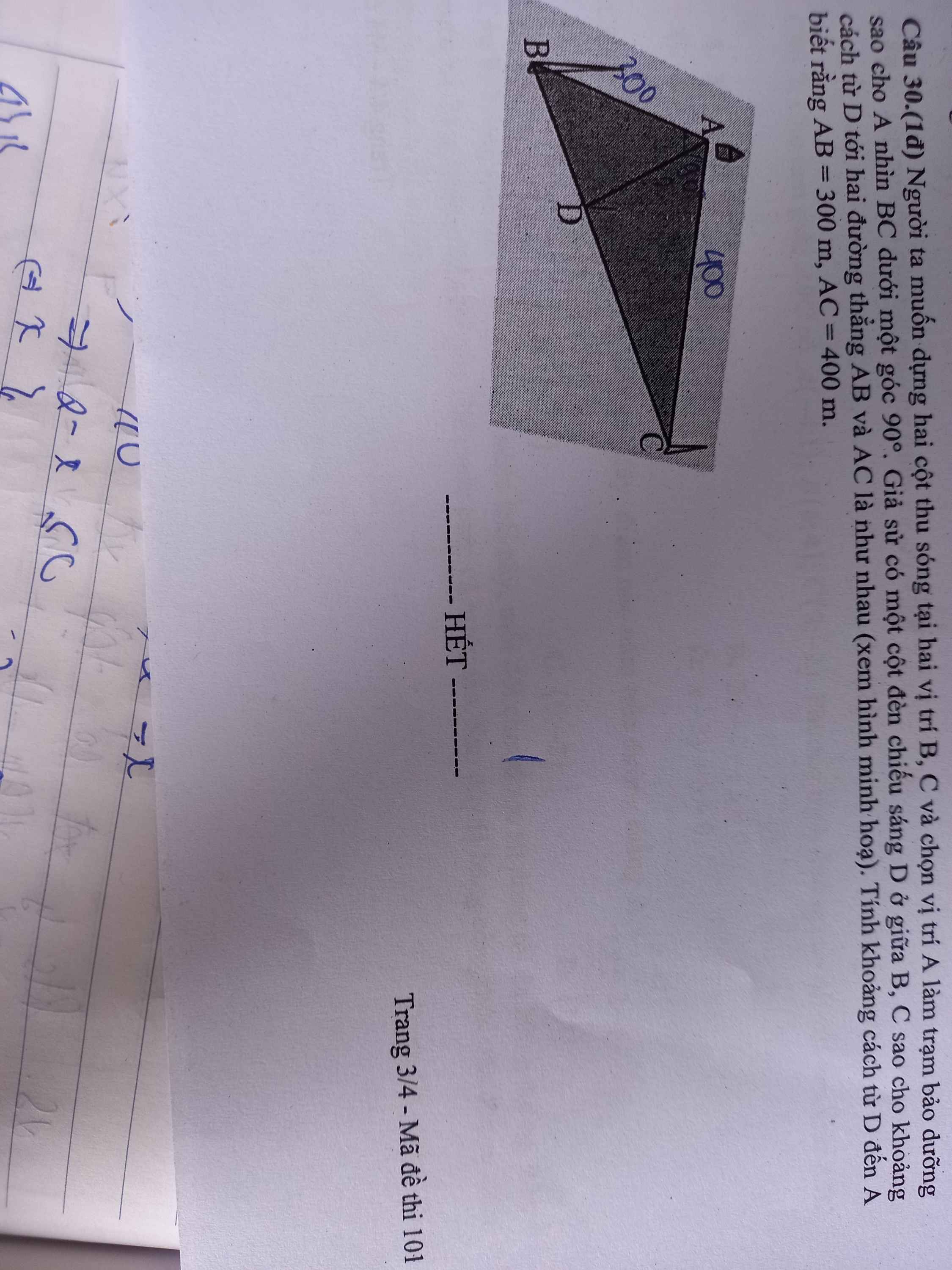
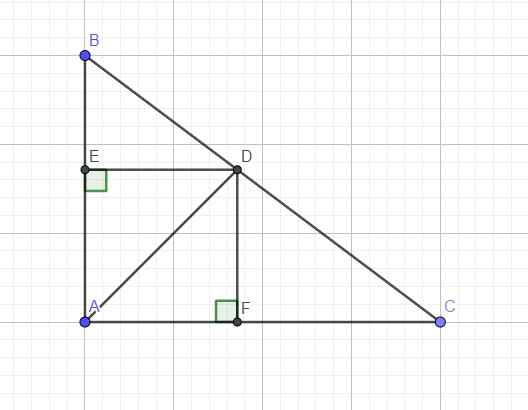
Từ D lần lượt kẻ DE vuông góc AB và DF vuông góc AC
\(\Rightarrow DE=DF\) (theo giả thiết)
\(\Rightarrow\)Tứ giác AEDF là hình vuông (có 3 góc vuông và 2 cạnh kề bằng nhau)
\(\Rightarrow AD\) là đường chéo đồng thời là phân giác góc A
\(BC=\sqrt{AB^2+AC^2}=500\left(m\right)\)
Áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{DC}{AC}\Leftrightarrow\dfrac{BD}{300}=\dfrac{500-BD}{400}\Rightarrow BD=\dfrac{1500}{7}\left(m\right)\)
Áp dụng Talet cho tam giác ABC:
\(\dfrac{BD}{BC}=\dfrac{DE}{AC}\Rightarrow DE=\dfrac{BD.AC}{BC}=\dfrac{1200}{7}\left(m\right)\)
\(\Rightarrow AD=DE\sqrt{2}\approx242,44\left(m\right)\)
 iải chi tiết hộ em với
iải chi tiết hộ em với  Giải chi tiết hộ em với ạ
Giải chi tiết hộ em với ạ 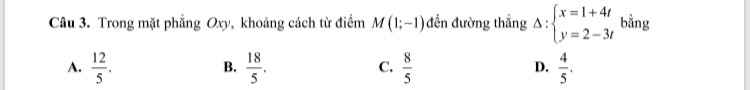






Pt đã cho có nghiệm duy nhất khi và chỉ khi:
\(m^2-4\ne0\Rightarrow m\ne\pm2\)
\(\Rightarrow\) Có \(5-\left(-5\right)+1-2=9\) giá trị nguyên của m