
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Pt đã cho có nghiệm duy nhất khi và chỉ khi:
\(m^2-4\ne0\Rightarrow m\ne\pm2\)
\(\Rightarrow\) Có \(5-\left(-5\right)+1-2=9\) giá trị nguyên của m


a: Tham số là 2m-1
Ẩn số là x
b: Tham số là n
Ẩn số là x


7: \(=\dfrac{1-sin\left(\dfrac{pi}{2}-x\right)}{1+cosx}=\dfrac{1-cosx}{1+cosx}\)
1:
\(=\dfrac{cos^2x-sin^2x}{cosx+sinx}=cosx-sinx\)
2:
\(=\dfrac{cos^22x-sin^22x}{cos2x-sin2x}=cos2x+sin2x\)

ĐK: \(x\ge0\)
Dễ thấy \(1-\sqrt{2\left(x^2-x+1\right)}\le1-\sqrt{2}< 0\)
Khi đó bất phương trình tương đương:
\(x-\sqrt{x}\le1-\sqrt{2\left(x^2-x+1\right)}\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(x+\dfrac{1}{x}-1\right)}\le0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2+2}\le0\)
\(\Leftrightarrow t-1+\sqrt{2t^2+2}\le0\)

Xét phương trình đã cho. Ta có \(VT=\sqrt{3\left(x+1\right)^2+1}\ge1;VP=2-2x-x^2=1-\left(x+1\right)^2\le0\) nên \(VT\ge VP\).
Đẳng thức xảy ra khi và chỉ khi \(x+1=0\Leftrightarrow x=-1\).
Vậy nghiệm của phương trình là x = -1.

a, x+7=-12
\(\Leftrightarrow\) x= -19
b, x-15=-21
\(\Leftrightarrow\) x= -6
c, 13-x=20
\(\Leftrightarrow\) x=-7

\(2x^2+y^2-6x+2xy-2y+5=0\)
\(\Leftrightarrow\left(x^2-4x+4\right)+\left(x^2+2xy+y^2\right)-\left(2x+2y\right)+1=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(x+y\right)^2-2\left(x+y\right)+1=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(x+y-1\right)^2=0\)
Mà \(\left(x-2\right)^2+\left(x+y-1\right)^2\ge0\forall x,y\)
Suy ra xảy ra khi \(\left\{{}\begin{matrix}\left(x-2\right)^2=0\\\left(x+y-1\right)^2=0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x-2=0\\x+y-1=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y+1=0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)
Vậy pt có nghiệm là \(\left(x;y\right)=\left(2;-1\right)\)
 Giải chi tiết hộ em với ạ
Giải chi tiết hộ em với ạ 
 iải chi tiết hộ em với
iải chi tiết hộ em với 

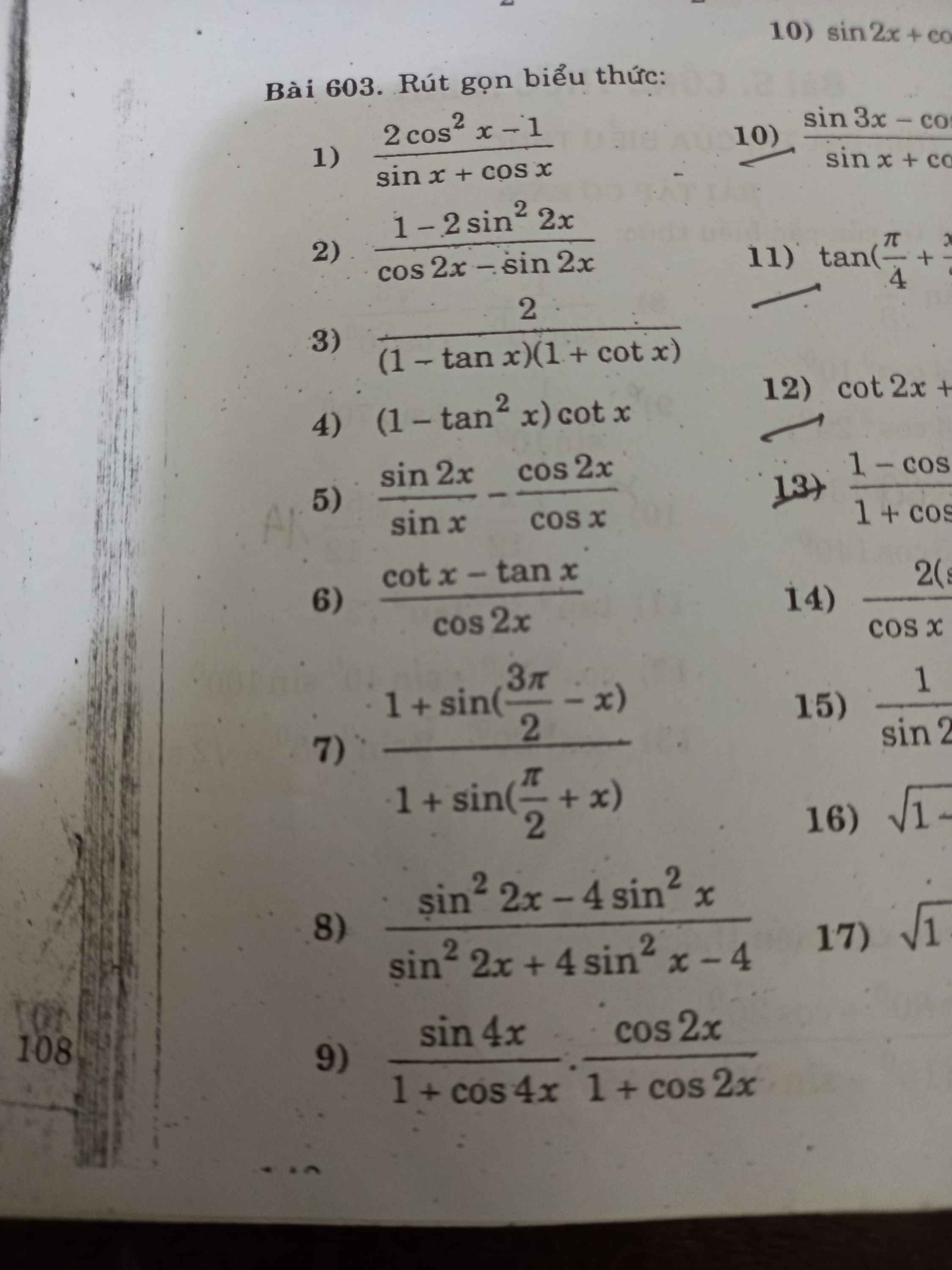

 Gải chi tiết hộ em ạ Cảm ơn !
Gải chi tiết hộ em ạ Cảm ơn !
ĐKXĐ: \(-1\le x\le4\)
\(\Leftrightarrow\left(x-3\right)\sqrt{1+x}-\left(x-3\right)+x-x\sqrt{4-x}=2x^2-6x\)
\(\Leftrightarrow\left(x-3\right)\left(\sqrt{1+x}-1\right)+x\left(1-\sqrt{4-x}\right)=2x^2-6x\)
\(\Leftrightarrow\dfrac{x\left(x-3\right)}{\sqrt{1+x}+1}+\dfrac{x\left(x-3\right)}{1+\sqrt{4-x}}=2\left(x^2-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x=0\Rightarrow x=...\\\dfrac{1}{\sqrt{1+x}+1}+\dfrac{1}{1+\sqrt{4-x}}=2\left(1\right)\end{matrix}\right.\)
Xét (1), do \(VT< \dfrac{1}{1}+\dfrac{1}{1}=2\Rightarrow VT< VP\Rightarrow\left(1\right)\) vô nghiệm
Vậy ...