Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt a=\(\sqrt{x^2+1}\)
=>a2=x2+1
Ta có hpt: \(\begin{cases}\left(1+xa\right)\left(a-x\right)=1\\a^2=x^2+1\end{cases}\Leftrightarrow\begin{cases}a-x+xa^2-x^2a=1\\a^2-x^2=1\end{cases}\)
\(\Leftrightarrow\begin{cases}a-x+xa^2-ax^2=1\\a^2-x^2=1\end{cases}\)
=>a-x+xa2-ax2=a2-x2
<=>(a-x)(1+xa-a-x)=0
<=>(a-x)(1-a)(1-x)=0
<=>*a=x *a=1 *x=1
<=>x2+1=x <=>\(\sqrt{x^2+1}\)=1
<=>x2-x+1=0(vô lí) <=>x2+1=1
<=>x2=0
<=>x=0
Vậy S={0;1}
\(1+x\sqrt{x^2+1}=\frac{1}{\sqrt{x^2+1}-x}\)
\(1+x\sqrt{x^2+1}=\sqrt{x^2+1}+x\) (nhân tử và mẫu vế phải với biểu thức liên hợp của mẫu số)
\(\sqrt{x^2-1}\left(x-1\right)-\left(x-1\right)=0\)
\(\left(x-1\right)\left(\sqrt{x^2+1}-1\right)=0\)
\(x=1\) hoặc \(\sqrt{x^2+1}=1\)
x=1 hoặc x =0


ĐKXD: x, y > 0.
\(Pt_{\left(1\right)}\Leftrightarrow\dfrac{y+\sqrt{x}}{x}=\dfrac{2\left(y+\sqrt{x}\right)}{y}\Leftrightarrow\left(y+\sqrt{x}\right)\left(\dfrac{1}{x}-\dfrac{2}{y}\right)=0\)
\(\Rightarrow y=2x\), thế vào Pt(2): \(2x\left(\sqrt{x^2+1}-1\right)=\sqrt{3x^2+3}\)
Đặt \(\sqrt{x^2+1}=a\) thì \(\left\{{}\begin{matrix}2x\left(a-1\right)=\sqrt{3}a\\a^2-x^2=1\end{matrix}\right.\)
Giải ra ta được \(\left(a-2\right)\left(4a^3-3a+2\right)=0\) nhưng vì \(a\ge1\) nên a=2
Do đó \(x=\pm\sqrt{3}\). Vậy (x, y)=...

\(1)\sqrt{x^2+1}< 3.\\ \Leftrightarrow x^2+1< 9.\\ \Leftrightarrow x^2< 8.\\ \Leftrightarrow\left[{}\begin{matrix}x< 2\sqrt{2}.\\x>-2\sqrt{2}.\end{matrix}\right.\)
\(\Leftrightarrow-2\sqrt{2}< x< 2\sqrt{2}.\)
\(2)\dfrac{x^2-4x+3}{x^2-4}< 0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-4x+3}{x^2-4}.\)
\(x^2-4=0.\Leftrightarrow\left[{}\begin{matrix}x=2.\\x=-2.\end{matrix}\right.\\ x^2-4x+3=0.\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=1.\end{matrix}\right.\)
Bảng xét dấu:
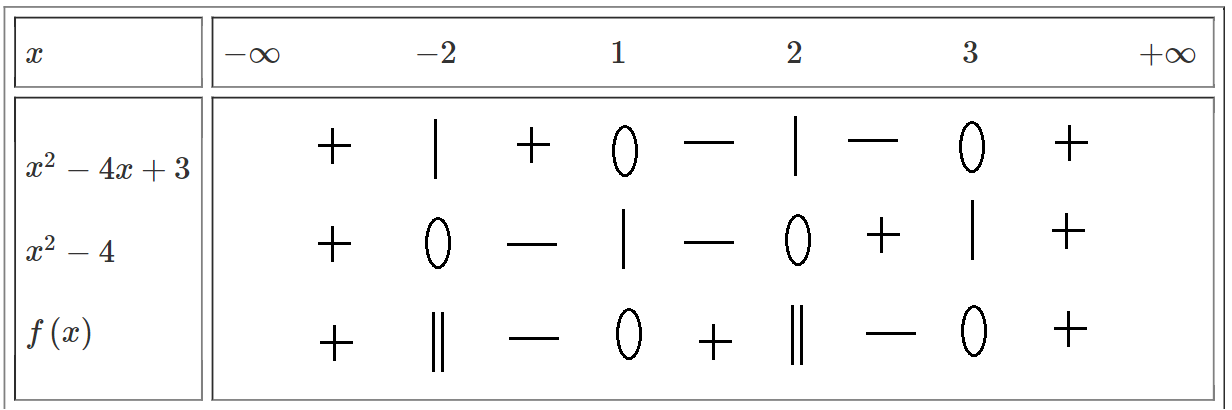
\(\Rightarrow f\left(x\right)< 0\Leftrightarrow x\in\left(-2;1\right)\cup\left(2;3\right).\)
Lời giải:
1.
$\sqrt{x^2+1}<3$
$\Leftrightarrow 0\leq x^2+1<9$
$\Leftrightarrow x^2+1<9$
$\Leftrightarrow x^2<8$
$\Leftrightarrow -2\sqrt{2}< x< 2\sqrt{2}$
2.
Xét 2 TH:
TH1: \(\left\{\begin{matrix} x^2-4x+3<0\\ x^2-4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x-1)(x-3)<0\\ (x-2)(x+2)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 1< x< 3\\ x>2 \text{hoặc} x<-2\end{matrix}\right.\)
\(\Leftrightarrow 2< x<3\)
TH2: \(\left\{\begin{matrix} x^2-4x+3>0\\ x^2-4<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x-1)(x-3)>0\\ (x-2)(x+2)<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>3 \text{hoặc} x<1\\ -2< x< 2\end{matrix}\right.\)
\(\Leftrightarrow -2< x< 1\)
Kết hợp 2 TH suy ra tập nghiệm \(S=(2;3)\cup (-2;1)\)



\(\sqrt{x^2+6x+9}=\left|2x-1\right|\Leftrightarrow\sqrt{\left(x+3\right)^2}=\left|2x-1\right|\)
\(\Leftrightarrow\left|x+3\right|=\left|2x-1\right|\Leftrightarrow\left(\left|x+3\right|\right)^2=\left(\left|2x-1\right|\right)^2\)
\(\Leftrightarrow\left(x+3\right)^2=\left(2x-1\right)^2\Leftrightarrow x^2+6x+9=4x^2-4x+1\)
\(\Leftrightarrow x^2+6x+9-4x^2+4x-1=0\Leftrightarrow-3x^2+10x+8=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\x=-\dfrac{2}{3}\end{matrix}\right.\)
thử lại ta thấy cả 2 nghiệm đều thỏa mãn phương trình đầu
vậy \(4;-\dfrac{2}{3}\) đều là nghiệm của phương trình đầu
vậy \(x=4;x=-\dfrac{2}{3}\)

Câu a:
ĐKXĐ: \(x\neq \pm 3\)
\(\left|\frac{x+5}{-x^2+9}\right|=2\Rightarrow \left[\begin{matrix} \frac{x+5}{-x^2+9}=2\\ \frac{x+5}{-x^2+9}=-2\end{matrix}\right.\)
\(\Rightarrow \left[\begin{matrix} x+5=2(-x^2+9)\\ x+5=-2(-x^2+9)\end{matrix}\right.\Rightarrow \left[\begin{matrix} 2x^2+x-13=0\\ 2x^2-x-23=0\end{matrix}\right.\)
\(\Rightarrow \left[\begin{matrix} x=\frac{-1\pm \sqrt{105}}{4}\\ x=\frac{1\pm \sqrt{185}}{4}\end{matrix}\right.\) (đều thỏa mãn )
Vậy.......
Câu b:
ĐKXĐ: \(x< 2\)
Ta có: \(\frac{4}{\sqrt{2-x}}-\sqrt{2-x}=2\)
\(\Rightarrow 4-(2-x)=2\sqrt{2-x}\)
\(\Leftrightarrow 4=(2-x)+2\sqrt{2-x}\)
\(\Leftrightarrow 5=(2-x)+2\sqrt{2-x}+1=(\sqrt{2-x}+1)^2\)
\(\Rightarrow \sqrt{2-x}+1=\sqrt{5}\) (do \(\sqrt{2-x}+1>0\) )
\(\Rightarrow \sqrt{2-x}=\sqrt{5}-1\)
\(\Rightarrow 2-x=6-2\sqrt{5}\)
\(\Rightarrow x=-4+2\sqrt{5}\) (thỏa mãn)
Vậy...........