Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Xét tam giác EIA vuông tại I nên :
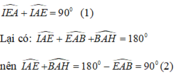
+) Xét hai tam giác ABH và ∆EAI có:
AB = AE ( vì ABDE là hình vuông)
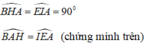
Suy ra: ∆ABH = ∆ EAI ( cạnh huyền – góc nhọn)
⇒ AH = EI ( hai cạnh tương ứng)
+) Tương tự hai tam giác vuông ACH và GAJ bằng nhau.
⇒ AH = GJ.
Suy ra EI = AH = GJ.
+) Xét ΔEKI và ΔGKJ có:
EI = GJ ( chứng minh trên)
∠(IKE) = ∠(JKG) (đối đỉnh).
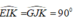
do đó ΔEKI = ΔGKJ ( cgv – gn)
suy ra: KE = KG
Từ đó ta có K trung điểm của EG. Vậy AK là trung tuyến của tam giác AEG.

Lập luận tương tự câu c), ta có BF là một đường cao của tam giác LBC.
Vậy ba đường thẳng AH, BF, CD là ba đường cao của tam giác LBC nên chúng đồng quy.

Xét tam giác ALB và ∆BCD có:
AL = BC ( chứng minh b)
AB = BD ( vì ABDE là hình vuông)
∠(BAL) = 90º + ∠(EAL) = 90 + ∠(ABC) = ∠(DBC) .
Suy ra: ∆ALB = ∆BCD ( c.g.c)
Suy ra ∠(ALB) = ∠(BCD) .
Mặt khác ta có ∠(ALB) + ∠(LBH) = 90º nên ∠(BCD) + ∠(LBH) = 90º.
Suy ra LB ⊥ CD, tức CD là một đường cao của tam giác LBC.

Nói chính xác luôn là tam giác vuông cân, lại bày hình vuông chi
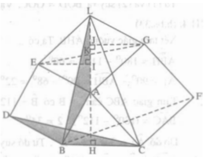
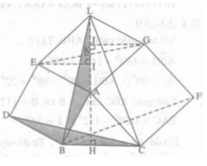
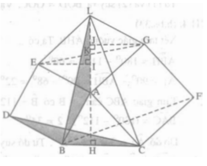
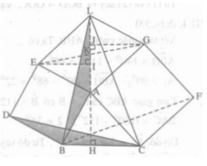
Theo a) ΔEKI = ΔGKJ nên KI = KJ.
Mặt khác, theo giả thiết K là trung điểm của AL nên KA = KL.
Suy ra: KA – KI = KL – KJ hay IA= JL.
Ta có: ∆ACH= ∆ GAJ ( theo a) nên HC = AJ;
∆ABH = ∆ EAI nên BH = AI.
+) Suy ra:
AL = AJ + JL = AJ + AI = HC + HB = BC