Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

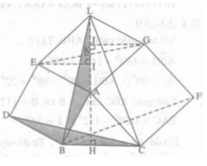
Lập luận tương tự câu c), ta có BF là một đường cao của tam giác LBC.
Vậy ba đường thẳng AH, BF, CD là ba đường cao của tam giác LBC nên chúng đồng quy.

+) Xét tam giác EIA vuông tại I nên :
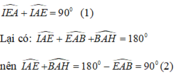
+) Xét hai tam giác ABH và ∆EAI có:
AB = AE ( vì ABDE là hình vuông)
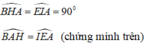
Suy ra: ∆ABH = ∆ EAI ( cạnh huyền – góc nhọn)
⇒ AH = EI ( hai cạnh tương ứng)
+) Tương tự hai tam giác vuông ACH và GAJ bằng nhau.
⇒ AH = GJ.
Suy ra EI = AH = GJ.
+) Xét ΔEKI và ΔGKJ có:
EI = GJ ( chứng minh trên)
∠(IKE) = ∠(JKG) (đối đỉnh).
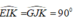
do đó ΔEKI = ΔGKJ ( cgv – gn)
suy ra: KE = KG
Từ đó ta có K trung điểm của EG. Vậy AK là trung tuyến của tam giác AEG.

a)Ta có: \(\widehat{AHB=90^O}\)
Theo tính chất goác ngoài của tam giác ta có:
\(\widehat{IAB}\)= \(\widehat{AHB}\)+ \(\widehat{HBA}\)= \(90^o\)+\(\widehat{HBA}\)=\(\widehat{EBA}\)+ \(\widehat{HBA}\)= \(\widehat{CBE}\)
xét xem tam giác ABI và BEC có
AI = BC (gt)
BA= EB( gt)
\(\widehat{IAB}\)= \(\widehat{CBE}\)(cmt)
\(\Rightarrow\Delta ABI\)= \(\Delta BEC\)( c - g - c )
a) Do \(\Delta ABI\)=\(\Delta BEC\)\(\Rightarrow\)\(BI\)=\(EC\)
Gọi giao điểm của EC với AB và BI lần lượt là J và K
\(\Delta ABI\)= \(\Delta BEC\)\(\Rightarrow\)\(\widehat{KBJ}\)= \(\widehat{BEK}\)
Vậy thì \(\widehat{KBJ}\)+ \(\widehat{KJB}\)= \(\widehat{BEK}\)+ \(\widehat{KJB}\)= \(90^O\)
Suy ra \(\widehat{BKJ}\)=\(90^O\)hay \(BI\)\(\)vuông góc với \(CE\)
c) Chứng minh hoàn toàn tương tự ta có: \(IC\)vuông góc với \(BF\)
Gọi giao điểm IC và BF là T.
Xét xem tam giác IBC có IH , CK, BT là đường cao nên chúng đồng quy tại 1 điểm .
Vậy AH, EC, BF đồng quy tại 1 điểm

a: BC=15cm
b: Xét ΔABM có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔABM cân tại B
c: Xét tứ giác ABNC có
K là trung điểm của BC
K là trung điểm của AN
Do đó: ABNC là hình bình hành
Suy ra: CN=AB
mà AB=BM
nên CN=BM
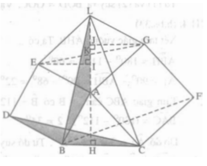
Nói chính xác luôn là tam giác vuông cân, lại bày hình vuông chi
nếu có ai k mình thì nhớ nhắn tin cho mình biết để mình k lại nha