
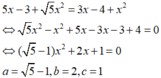
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

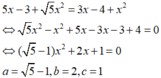

a: \(\Leftrightarrow4x^2-3x+7=0\)
a=4; b=-3; c=7
b: \(\Leftrightarrow\sqrt{5}x^2-x^2+5x-3-3x+4=0\)
\(\Leftrightarrow x^2\cdot\left(\sqrt{5}-1\right)+2x+1=0\)
\(a=\sqrt{5}-1;b=2;c=1\)
c: \(\Leftrightarrow mx^2-x^2-3x+mx+5=0\)
\(\Leftrightarrow x^2\left(m-1\right)+x\left(m-3\right)+5=0\)
a=m-1; b=m-3; c=5
d: \(\Leftrightarrow m^2x^2-x^2+x+m-mx-m-2=0\)
\(\Leftrightarrow x^2\left(m^2-1\right)+x\left(1-m\right)-2=0\)
\(a=m^2-1;b=1-m;c=-2\)

4 x 2 + 2x = 5x - 7 ⇔ 4 x 2 - 3x + 7 = 0 có a = 4, b = -3, c = 7

m x 2 - 3x + 5 = x 2 - mx ⇔ ⇔ (m - 1) x 2 - (3 - m)x + 5 = 0
m - 1 ≠ 0
nó là phương trình bậc hai có a = m – 1; b = - (3 – m ); c = 5

a ) 5 x 2 + 2 x = 4 − x ⇔ 5 x 2 + 2 x + x − 4 = 0 ⇔ 5 x 2 + 3 x − 4 = 0
Phương trình bậc hai trên có a = 5; b = 3; c = -4.
b)
3 5 x 2 + 2 x − 7 = 3 x + 1 2 ⇔ 3 5 x 2 + 2 x − 3 x − 7 − 1 2 = 0 ⇔ 3 5 x 2 − x − 15 2 = 0
c)
2 x 2 + x − 3 = x ⋅ 3 + 1 ⇔ 2 x 2 + x − x ⋅ 3 − 3 − 1 = 0 ⇔ 2 x 2 + x ⋅ ( 1 − 3 ) − ( 3 + 1 ) = 0
Phương trình bậc hai trên có a = 2; b = 1 - √3; c = - (√3 + 1).
d)
2 x 2 + m 2 = 2 ( m − 1 ) ⋅ x ⇔ 2 x 2 − 2 ( m − 1 ) ⋅ x + m 2 = 0
Phương trình bậc hai trên có a = 2; b = -2(m – 1); c = m 2
Kiến thức áp dụng
Phương trình bậc hai một ẩn là phương trình có dạng: ax2 + bx + c = 0
trong đó x được gọi là ẩn; a, b, c là các hệ số và a ≠ 0.

5x2 + 2x = 4 – x
⇔ 5x2 + 2x + x – 4 = 0
⇔ 5x2 + 3x – 4 = 0
Phương trình bậc hai trên có a = 5; b = 3; c = -4.

2x2 + x - √3 = x.√3 + 1
⇔ 2x2 + x - x.√3 - √3 – 1 = 0
⇔ 2x2 + x.(1 - √3) – (√3 + 1) = 0
Phương trình bậc hai trên có a = 2; b = 1 - √3; c = - (√3 + 1).

Giải
a) Ta có : 2.x2 -2.x = 5.x
<=> 2.x2 -3.x-5=0 : a = 2 ; b = 3 ; c = -5
b) Ta có : x2 +2.x = m. x + m
<=> x2 + ( 2-m ) .x - m = 0 : a = 1 ; b=2-m ; c=-m
c) Ta có : 2.x2 \(+\sqrt{2}.\left(3.x-1\right)=1+\sqrt{2}\)
<=> 2.x2 + 3.\(\sqrt{2}.x-2.\sqrt{2}-1=0\): a = 2 ; b= 3\(\sqrt{2};c=-2\sqrt{2}-1\)
a) \(2x^2-2x=5+x\)
\(\Leftrightarrow2x^2-x-5=0\)với \(\hept{\begin{cases}a=2\\b=-3\\c=-5\end{cases}}\)
b) \(x^2+2x=mx+m\)
\(\Leftrightarrow x^2+\left(2-m\right)x-m=0\)với \(\hept{\begin{cases}z=1\\b=3-m\\c=-m\end{cases}}\)
c) \(2x^2+\sqrt{2}\left(3x-1\right)=1+\sqrt{2}\)
\(\Leftrightarrow2x^2+3\sqrt{2}\cdot x-2\sqrt{2}-1=0\)
với \(\hept{\begin{cases}a=2\\b=3\sqrt{2}\\c=-2\sqrt{2}-1\end{cases}}\)

a) 5x2 + 2x = 4 – x ⇔ 5x2 + 3x – 4 = 0; a = 5, b = 3, c = -4
b) x2 + 2x – 7 = 3x +
⇔
x2 – x -
= 0, a =
, b = -1, c = -
c) 2x2 + x - √3 = √3 . x + 1 ⇔ 2x2 + (1 - √3)x – 1 - √3 = 0
Với a = 2, b = 1 - √3, c = -1 - √3
d) 2x2 + m2 = 2(m – 1)x ⇔ 2x2 - 2(m – 1)x + m2 = 0; a = 2, b = - 2(m – 1), c = m2