Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi z = a + bi. Dễ dàng chứng minh được ![]()
Ta có
w
=
12
-
5
i
z
¯
+
3
i
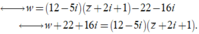
Lấy môđun hai vế, ta được ![]()
Biểu thức ![]() chứng tỏ tập hợp các số phức w là một đường tròn có tâm I(-22;-16) và bán kính r = 52.
chứng tỏ tập hợp các số phức w là một đường tròn có tâm I(-22;-16) và bán kính r = 52.
Chọn C.

Đáp án A
Giả sử z = x + y i
Ta có z - 1 + i = z + 2 i ⇔ x - 1 2 + y - 1 2 = x 2 + y + 2 2 ⇔ x + 3 y + 1 = 0
Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z - 1 + i = z + 2 i là đường thẳng

2 + i z = 10 z + 1 - 2 i
⇔ 2 z - 1 + z + 2 i = 10 z 2 z
Bình phương modun của số thức bên trái và bên phải bằng nhau ta có:
⇔ 2 z - 1 + z + 2 i = 10 z 2 z
= 10 z 2 ⇔ 5 z 2 + 5 = 10 z 2 ⇒ z = 1
Đặt w = x + yi ⇒ w = (3 - 4i )z+2i
⇔ (x + 1 ) + ( y - 2 )i = ( 3 - 4i )z
⇒ x + 1 2 + y - 2 2 = 25
Vậy I ( -1;2 ), R = 5
Đáp án cần chọn là C
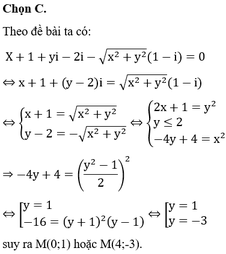
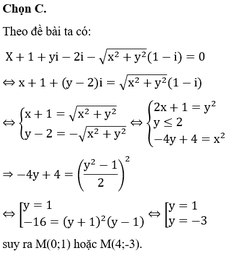
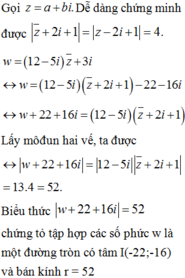

Chọn đáp án A