Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có
u n + 1 = 1 + 1 2 2 + 1 3 2 + ... + 1 n 2 + 1 n + 1 2 = u n + 1 n + 1 2 > u n ,
vậy dãy số đã cho là dãy số tăng.
Hơn nữa vì dãy số là tổng các số dương nên bị chặn dưới bởi 0, ta chỉ cần kiểm tra dãy số có bị chặn trên hay không là đủ để chọn phương án đúng.
Ta có
1 2 2 < 1 1.2 = 1 − 1 2 1 3 2 < 1 2.3 = 1 2 − 1 3 .......................... 1 n 2 < 1 n − 1 . n = 1 n − 1 − 1 n
Vì vậy u n < 2 − 1 n < 2 , do đó dãy số bị chặn trên.

Xét đáp án A ta có:
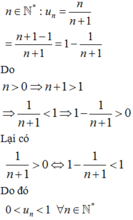
Vậy dãy số u n = n n + 1 là dãy số bị chặn.
Chọn A.

Đáp án A
Phương pháp:1
- Dãy số u n được gọi là bị chặn nếu nó vừa bị chặn trên, vừa bị chặn dưới, nghĩa là: tồn tại số m, M sao cho m ≤ u n ≤ M , ∀ n ∈ ℕ *
Chú ý: Nếu lim u n = ± ∞ thì ta kết luận ngay dãy không bị chặn.
Cách giải:
Đáp án A: 0 < u n = 2 n + 1 n + 1 = 2 n + 1 − 1 n + 1 = 2 − 1 n + 1 < 2 , ∀ n ∈ ℕ * nên u n là dãy bị chặn.
Đáp án B, C, D: lim u n = + ∞ nên các dãy số này đều không là dãy bị chặn.

Đáp án B
lim n → + ∞ 2 n + 1 n − 1 = 2 do đó dãy số này bị chặn.

Đáp án A
Ta có: 0 < u n < 1 1.2 + 1 2.3 + ... + 1 n n + 1 = 1 − 1 n + 1 < 1
Dãy u n bị chặn.

Đáp án C
Ta có u n = n n + 1 = 1 − 1 n + 1 < 1 ; u n > 0 do đó dãy số u n = n n + 1 là dãy số nào bị chặn

1 . giải
Thương của phép chia đó là: 135 : 15 = 9
Đáp số : 9.
2 . giải
Số đó khi giảm đi 4 lần có kết quả là: 460 : 5 = 92
Số cần tìm là: 92 x 4 = 368
Đáp số : 368
3 . giải
Tìm nửa chu vi. => chính là tổng của chiều dài và chiều rộng.
giải bài toán theo dạng tổng hiệu
tìm được chiều dài và chiều rộng => tìm diện tích.
Nửa chu vi: 320 : 2 = 160 (cm)
Vẽ sơ đồ tổng hiệu với tổng là 160 cm, hiệu là 20 cm
Chiều rộng hình chữ nhật là: (160 - 20 ): 2 = 70 (cm)
Chiều dài hình chữ nhật là: 70 + 20 = 90 (cm)
Diện tích hình chữ nhật là: 90 x 70 = 6300 (cm2)
Đáp số : 6300 cm2
1/ Mình không biết giải
2/Số đó khi giảm đi 4 lần có kết quả là: 460 : 5 = 92
Số cần tìm là: 92 x 4 = 368
3/Tìm nửa chu vi. -> chính là tổng của chiều dài và chiều rộng.
giải bài toán theo dạng tổng hiệu
tìm được chiều dài và chiều rộng -> tìm diện tích.
Nửa chu vi: 320 : 2 = 160 (cm)
Vẽ sơ đồ tổng hiệu với tổng là 160 cm, hiệu là 20 cm
Chiều rộng hình chữ nhật là: (160 - 20 ): 2 = 70 (cm)
Chiều dài hình chữ nhật là: 70 + 20 = 90 (cm)
Diện tích hình chữ nhật là: 90 x 70 = 6300 (cm2)

Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)

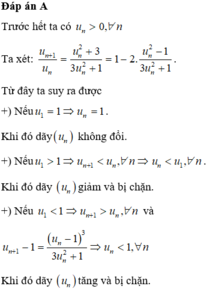
Ta có
u n + 1 = u n + u n - 1 ⇒ u 3 = u 2 + u 1 = 3 + 2 > 3 = u 2
⇒ u 4 = u 3 + u 2 > u 2 + u 1 = u 3
Theo nguyên lý quy nạp ta có là dãy tăng
là dãy tăng
u n + 1 = u n + u n - 1 < 2 u n + 1 ⇔ u n + 1 2 < 4 u n + 1 ⇔ 0 < u n + 1 < 4
Vậy u n tăng và bị chặn.
Đáp án cần chọn là A