Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(1) Suy ra a là số lẻ ( vì nếu a là số chẵn thì a.b.c.dlaf số chẵn mà chẵn cộng chẵn bằng chẵn do đó a là số lẻ )
Cũng như vậy, các trường hợp 2 , 3 , 4 đều là số lẻ.
Vì lẻ nhân lẻ nhân lẻ nhân lẻ nhân lẻ bằng số lẻ mà lẻ cộng lẻ bằng chẵn nên không có trường hợp 1,2,3,4.


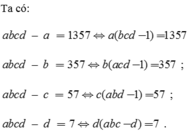
Nếu 1 trong a,b,c,d chẵn thì 1 trong 4 đẳng thức sai (kết quả ra chẵn do 1 số chẵn nhân 1 tích thì chẵn) =>a,b,c,d không tồn tại (do a,b,c,d phải thoả cả 4 đẳng thức)
Nếu a,b,c,d đều lẻ thì 1số lẻ nhân cho 1 số chẵn (tích 3 số lẻ trừ 1 thì chẵn) thì là một số chẵn=>a,b,c,d không tồn tại
Vậy không tồn tại các số nguyên a,b,c,d để thoả yêu cầu đề bài

nhận xét : +, các số 2019 , 1999, 2021 đều là số lẻ .
+, tổng của 2 số lẻ là lẻ thì 2 số đó khác tính chẵn lẻ.
do đó : nếu abcd thì từ \(\left(1\right)\)\(a\Rightarrow lẻ\)
tương tự \(\left(2\right),\left(3\right),\left(4\right)\)ta có b , c , d cũng là số lẻ.
mà a,b,c,d đều là chẵn . khi đó abcd là số chẵn . mâu thuẫn.
vậy ko có các số nguyên a,b,c,d thoả mãn 4 đều kiện trong đề bài.
Sửa lại 2010 thành 2021