Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


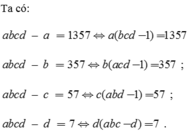
Nếu 1 trong a,b,c,d chẵn thì 1 trong 4 đẳng thức sai (kết quả ra chẵn do 1 số chẵn nhân 1 tích thì chẵn) =>a,b,c,d không tồn tại (do a,b,c,d phải thoả cả 4 đẳng thức)
Nếu a,b,c,d đều lẻ thì 1số lẻ nhân cho 1 số chẵn (tích 3 số lẻ trừ 1 thì chẵn) thì là một số chẵn=>a,b,c,d không tồn tại
Vậy không tồn tại các số nguyên a,b,c,d để thoả yêu cầu đề bài

(1) Suy ra a là số lẻ ( vì nếu a là số chẵn thì a.b.c.dlaf số chẵn mà chẵn cộng chẵn bằng chẵn do đó a là số lẻ )
Cũng như vậy, các trường hợp 2 , 3 , 4 đều là số lẻ.
Vì lẻ nhân lẻ nhân lẻ nhân lẻ nhân lẻ bằng số lẻ mà lẻ cộng lẻ bằng chẵn nên không có trường hợp 1,2,3,4.

ko tồn tại
chứng minh mà, i chả biết không tồn tại, ngu.