Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có: ![]()
Suy ra PTTT của (C) tại M là ![]()
Khi đó PT hoành độ giao điểm của (C) và ![]() là:
là: ![]()

+Đồ thị hàm số đã cho có TCĐ là x= 1 và TCN là y= 2; giao điểm của hai tiệm cận là
I (1; 2) .
Lấy điểm M ( a ; b ) ∈ C ⇒ b = 2 a - 1 a - 1 ( a > 1 ) .
+ Phương trình tiếp tuyến của (C ) tại M là y = - 1 ( a - 1 ) 2 ( x - a ) + 2 a - 1 a - 1
+ Phương trình đường thẳng MI là y = 1 ( a - 1 ) 2 ( x - 1 ) + 2
+ Tiếp tuyến tại M vuông góc với MI nên ta có
-
1
(
a
-
1
)
2
.
1
(
a
-
1
)
2
=
-
1
⇔
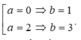
Vì yêu cầu hoành độ và tung độ của M nguyên dương nên điểm cần tìm là M( 2; 3).
Chọn D.

Chọn A.
Xét hàm số
y
=
x
4
2
-
3
x
2
+
5
2
ta có: ![]()
Phương trình tiếp tuyến của (C) tại M: 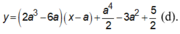
Phương trình hoành độ giao điểm của (d) và (C):
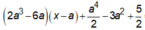
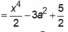
![]()
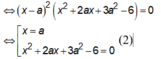
Đường thẳng (d) cắt (C) tại hai điểm phân biệt khác M khi phương trình (2_ có hai nghiệm phân biệt khác a
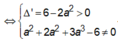
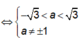
mà a nguyên nên a = 0.

Gọi k là hệ số góc của tiếp tuyến tại M, N thì \(x_M;x_N\) là nghiệm của phương trình :
\(f'\left(x\right)=k\Leftrightarrow3x^2-6x-k=0\)
Để tồn tại hai tiếp điểm M, N thì phải có \(\Delta'>0\Leftrightarrow k>-3\)
Ta có \(y=f'\left(x\right)\left(\frac{1}{3}x-\frac{1}{3}\right)-2x+2\)
Từ \(f'\left(x_M\right)=f'\left(x_N\right)=k\) suy ra phương trình đường thẳng MN là :
\(y=\left(\frac{k}{3}-2\right)x+2-\frac{k}{3}\), khi đó \(A\left(1;0\right);B\left(0;\frac{6-k}{3}\right)\)
Ta có \(AB^2=10\Leftrightarrow k=15\) (do k > -3)
Từ đó ta có 2 tiếp tuyến cần tìm là :
\(y=15x-12\sqrt{6}-15\)
\(y=15x+12\sqrt{6}-15\)




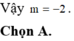

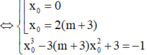
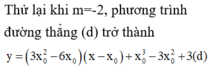

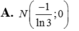
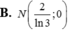
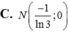
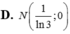




Hướng dẫn:
Ta có hàm số \(y=(x^2-4x+4)(x+1)=x^3-3x^2+4\) có đồ thị (C)
M nằm trên (C) , hoành độ dương nên có tọa độ \(M(a;a^3-3a^2+4)\) với \(a>0\)
Tính y' rồi lập viết phương trình tiếp tuyến của (C) tại điêm M, lập hệ phương trình giao điêm của tiếp tuyến với (C), tìm ra tọa độ 2 điểm M,N rồi thay vào điều kiện MN=3 đê ra kết quả
Chúc bạn học tốt ^^
Lập hệ phương trình giao điểm là như thế nào vậy bạn, lần đầu mình mới nghe :))