Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(q_1=q_2=16\mu C=16.10^{-6}m\)
\(q_0=4\mu C=4.10^{-6}m\)
a.
Hợp lực tác dụng lên q0: \(\vec{F}=\vec{F_{10}}+\vec{F_{20}}\)
Hai véc tơ ngược chiều, do vậy ta có độ lớn: \(F=F_{20}-F_{10}\) (1)
\(F_{10}=9.10^9\dfrac{16.10^{-6}.4.10^{-6}}{0,6^2}=1,6(N)\)
\(F_{20}=9.10^9\dfrac{16.10^{-6}.4.10^{-6}}{0,4^2}=3,6(N)\)
Thay vào (1) ta được: \(F=2(N)\)
b.
Do \(AB^2=AM^2+AN^2\) nên tam giác ABN vuông tại N
Hợp lực tác dụng lên q0: \(\vec{F'}=\vec{F_{10}}+\vec{F_{20}}\)
Hai véc tơ thành phần vuông góc với nhau, suy ra độ lớn:
\(F'=\sqrt{F_{10}^2+F_{20}^2}\) (2)
\(F_{10}=9.10^9\dfrac{16.10^{-6}.4.10^{-6}}{0,6^2}=1,6(N)\)
\(F_{20}=9.10^9\dfrac{16.10^{-6}.4.10^{-6}}{0,8^2}=0,9(N)\)Thay vào (2) ta được: \(F=1,84(N)\)
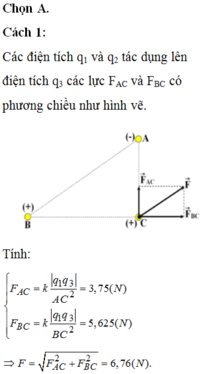
a, Lực điện tương tác giữa hai điện tích là
Fđ = \(9.10^9.\dfrac{\left|-10^{-7}.5.10^{-8}\right|}{0.05^2}=0.018\left(N\right)\)
b, Ta có AC2 + BC2 = AB2 (32 + 42 = 52) nên theo định lí đảo của định lí Pitago ta có tam giác vuông ABC tại C
Lực điện tổng hợp bằng 1 nửa lực điện ở câu A (vẽ hình là thấy)
độ lớn bằng 0.009 N
c, Mình chưa học, nhưng chắc chỉ cần dùng ct là xong

![]()
Giả sử q 0 > 0. Để q0 cân bằng thì hợp lực tác dụng lên q 0 phải bằng không, ta có:
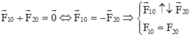
Vì q1; q2 cùng dấu nên C thuộc đoạn thẳng AB: AC + BC = AB (*) và q 1 A C 2 = q 2 B C 2 (**)
Từ (*) và (**) ta có:
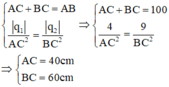


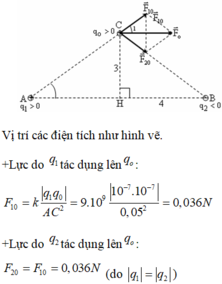

a, ta thấy AM+BM=AB
\(F_1=k.\dfrac{\left|q_1q_0\right|}{AM^2}=3,75\left(N\right)\)
\(F_2=k\dfrac{\left|q_2q_0\right|}{BM^2}=5,625\left(N\right)\)
\(\Rightarrow F=\left|F_1-F_2\right|=1,875\left(N\right)\)
b, để ý thấy \(AB^2=AN^2+BN^2\)
\(\Rightarrow F_1\perp F_2\)
\(F_1=k.\dfrac{\left|q_1q_0\right|}{AN^2}=3,75\left(N\right)\)
\(F_2=k.\dfrac{\left|q_2q_0\right|}{BN^2}=1,40625\left(N\right)\)
\(\Rightarrow F=\sqrt{F_1^2+F_2^2}\approx4\left(N\right)\)
c, ta thấy AI=BI=AB=1m
vecto lực tương tác là tam giác đêu \(\alpha=60^o\)
\(F_1=k\dfrac{\left|q_1q_0\right|}{AI^2}=1,35\left(N\right)\)
\(F_2=k.\dfrac{\left|q_2q_0\right|}{BI^2}=0,9\left(N\right)\)
\(\Rightarrow F=\sqrt{F_1^2+F_2^2+2F_1F_2cos\alpha}=...\)
QEZ, Lê Thị Thục Hiền CTV