LT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 6 2019
Xét tam giác ABC có I là tâm đường tròn nội tiếp
\(\Rightarrow S_{ABC}=S_{AIB}+S_{BIC}+S_{CIA}=\frac{1}{2}AB.r+\frac{1}{2}BC.r+\frac{1}{2}CA.r\)
\(=\frac{1}{2}\left(AB+BC+CA\right).r=p.r\)
\(\Rightarrow r=\frac{S_{ABC}}{p}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
Gọi D, E, F lần lượt là tiếp điểm của (O) với BC, AC, AB
\(\Rightarrow OD\perp BC\) ; \(OE\perp AC\) ; \(OF\perp AB\)
Và \(OD=OE=OF=R\)
Ta có:
\(S_{ABC}=S_{OAB}+S_{OAC}+S_{OBC}\)
\(=\dfrac{1}{2}OF.AB+\dfrac{1}{2}OE.AC+\dfrac{1}{2}OD.BC\)
\(=\dfrac{1}{2}R.AB+\dfrac{1}{2}R.AC+\dfrac{1}{2}R.BC\)
\(=\dfrac{1}{2}R.\left(AB+AC+BC\right)\)
\(\Rightarrow45=\dfrac{1}{2}R.30\)
\(\Rightarrow R=3\left(cm\right)\)
CM
31 tháng 12 2018
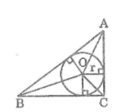
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBCv
Ta có : S A B C = S O A B + S O A C + S O B C
= (1/2).AB.r + (1/2).AC.r + (1/2).BC.r
= (1/2)(AB + AC + BC).r
Mà AB + AC + BC = 2p
Nên S A B C = (1/2).2p.r = p.r
12 tháng 8 2016
Gọi I,E,F lần lược là tiếp điểm của đường tròn tâm O nội tiếp với AB,BC,CA ta có OI = OE = OF = r
S ABC = S AOB + S BOC + S COA = AB.OI/2 + BC.OE/2 + CA.OF/2
= (AB + BC + CA).r/2 = pr
HH
9 tháng 8 2020
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBCv
Ta có : SABC = SOAB + SOAC + SOBC
\(=\left(\frac{1}{2}\right)AB.r+\left(\frac{1}{2}\right).AC.r+\left(\frac{1}{2}\right).BC.r\)
\(=\left(\frac{1}{2}\right)\left(AB+AC+BC\right).r\)
Mà AB + AC + BC = 2p
Nên \(S_{ABC}=\left(\frac{1}{2}\right).2p.r=p.r\)
29 tháng 6 2019
Gọi I là tâm đường tròn bàng tiếp góc A của tam giác ABC
Ta có:
SABC=SABI+SACI−SBIC
=Rb/2 + Rc/2 − Ra/ 2
=R. (b+c−a/2)
=R(p−a)
=> R = S/(p-a) (đpcm)
