Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi I là tâm đường tròn bàng tiếp góc A của tam giác ABC
Ta có:
SABC=SABI+SACI−SBIC
=Rb/2 + Rc/2 − Ra/ 2
=R. (b+c−a/2)
=R(p−a)
=> R = S/(p-a) (đpcm)

BÀI LÀM
a, xét tứ giác ADOE có:
góc A= góc E=góc D=90O
mà ta thấy: OE=OD( bán kính = nhau)
vậy tứ giác ADOE là hình vuông (dhnb)
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có SΔABC=SΔOAB+SΔOBC+SΔOAC
=12 OD.AB+12 OE.AC+12 OH.BC
=12 r.(AB+AC+BC)
=12 pr ( là chu vi của tam giác , là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: BC=√AB2+AC2=10(cm).
Diện tích tam giác ABC là: 12 AB.AC=12 .6.8=24(cm2).
Chu vi tam giác ABC là: 6+8+10=24(cm).
Suy ra: 24=12 .24.r⇔r=2(cm).

Giải chi tiết:
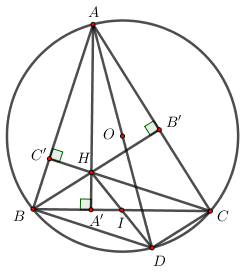
a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.
Xét tứ giác AB’HC’ có ∠AB′H+∠AC′H=900+900=1800⇒∠AB′H+∠AC′H=900+900=1800⇒ Tứ giác AB’HC’ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.
Ta có ∠ABD=900∠ABD=900 (góc nội tiếp chắn nửa đường tròn) ⇒AB⊥BD⇒AB⊥BD.
Mà CH⊥AB(gt)⇒BD∥CHCH⊥AB(gt)⇒BD∥CH
Chứng minh tương tự ta có CD∥BHCD∥BH.
⇒⇒ Tứ giác BHCD là tứ giác nội tiếp (Tứ giác có các cặp cạnh đối song song)
Mà BC∩HD=I(gt)⇒IBC∩HD=I(gt)⇒I là trung điểm của BC.
c) Tính AHAA′+BHBB′+CHCC′AHAA′+BHBB′+CHCC′.
Ta có:
SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′
Chứng minh tương tự ta có: BHBB′=1−SHACSABC;CHCC′=1−SHABSABCBHBB′=1−SHACSABC;CHCC′=1−SHABSABC
⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2
Xét tam giác ABC có I là tâm đường tròn nội tiếp
\(\Rightarrow S_{ABC}=S_{AIB}+S_{BIC}+S_{CIA}=\frac{1}{2}AB.r+\frac{1}{2}BC.r+\frac{1}{2}CA.r\)
\(=\frac{1}{2}\left(AB+BC+CA\right).r=p.r\)
\(\Rightarrow r=\frac{S_{ABC}}{p}\)