Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(n^2>n^2-n=n\left(n-1\right)\Rightarrow\dfrac{1}{n^2}< \dfrac{1}{n\left(n-1\right)}\Rightarrow\dfrac{1}{n^2}< \dfrac{1}{n-1}-\dfrac{1}{n}\)

\(VT=\dfrac{1}{5}\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{\left(5n+1\right)\left(5n+6\right)}\right)\)
\(=\dfrac{1}{5}\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-...+\dfrac{1}{5n+1}-\dfrac{1}{5n+6}\right)\)
\(=\dfrac{1}{5}\left(1-\dfrac{1}{5n+6}\right)\)
\(=\dfrac{1}{5}\cdot\dfrac{5n+6-1}{5n+6}\)
\(=\dfrac{n+1}{5n+6}=VP\)

Bài 3:
Để A là số nguyên thì \(n-2+5⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{3;1;7;-3\right\}\)

2) Theo đề, ta có: \(\dfrac{23+n}{40+n}=\dfrac{3}{4}\)
\(\Leftrightarrow4\left(n+23\right)=3\left(n+40\right)\)
\(\Leftrightarrow4n+92-3n-120=0\)
\(\Leftrightarrow n=28\)
Vậy: n=28
gọi UCLN của (30n+1,15n+2) là d 30n+1 chia hết cho d
suy ra:30n+1 chia hết cho d 15n+2 chia hết cho d
suy ra:30n+4 chia hết cho d (30n+4)-(30n+1) chia hết cho d
3 chia hết cho d vì 30n+1,15n+2 ko chia hết cho d
nên ucln =1 vậy ps 30n+1/15n+2 là ps tối giản

\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{\left(n-1\right)n}\)
\(=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(=1-\dfrac{1}{n}< 1\)
\(\Rightarrow\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< 1\left(đpcm\right)\)

\(S=\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{n\left(n+3\right)}\)
\(\Rightarrow S=\dfrac{4-1}{1.4}+\dfrac{7-4}{4.7}+\dfrac{10-7}{7.10}+...+\dfrac{\left(n+3\right)-n}{n\left(n+3\right)}\)
\(\Rightarrow S=\dfrac{4}{1.4}-\dfrac{1}{1.4}+\dfrac{7}{4.7}-\dfrac{4}{4.7}+\dfrac{10}{7.10}-\dfrac{7}{7.10}+...+\dfrac{n+3}{n\left(n+3\right)}-\dfrac{n}{n\left(n+3\right)}\)
\(\Rightarrow S=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{n}-\dfrac{1}{n+3}\)
\(\Rightarrow S=1-\dfrac{1}{n+3}< 1\Rightarrow S< 1\)
Vậy S < 1

a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: 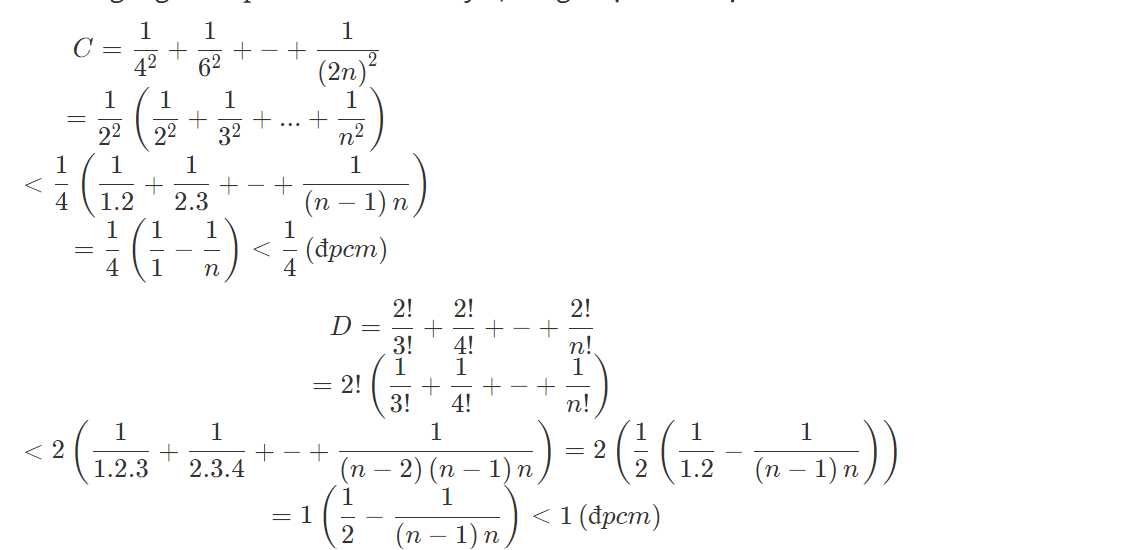

a) Vế trái \(=\dfrac{1.3.5...39}{21.22.23...40}=\dfrac{1.3.5.7...21.23...39}{21.22.23....40}=\dfrac{1.3.5.7...19}{22.24.26...40}\)
\(=\dfrac{1.3.5.7....19}{2.11.2.12.2.13.2.14.2.15.2.16.2.17.2.18.2.19.2.20}\\ =\dfrac{1.3.5.7.9.....19}{\left(1.3.5.7.9...19\right).2^{20}}=\dfrac{1}{2^{20}}\left(đpcm\right)\)
b) Vế trái
\(=\dfrac{1.3.5...\left(2n-1\right)}{\left(n+1\right).\left(n+2\right).\left(n+3\right)...2n}\\ =\dfrac{1.2.3.4.5.6...\left(2n-1\right).2n}{2.4.6...2n.\left(n+1\right)\left(n+2\right)...2n}\\ =\dfrac{1.2.3.4...\left(2n-1\right).2n}{2^n.1.2.3.4...n.\left(n+1\right)\left(n+2\right)...2n}\\ =\dfrac{1}{2^n}.\\ \left(đpcm\right)\)


Đề em ghi bị sai nhé, đề đúng phải là: \(\dfrac{1}{n^2}>\dfrac{1}{n}-\dfrac{1}{n+1}\)
Ta có: \(n^2< n^2+n=n\left(n+1\right)\Rightarrow\dfrac{1}{n^2}>\dfrac{1}{n\left(n+1\right)}\)
\(\Leftrightarrow\dfrac{1}{n^2}>\dfrac{1}{n}-\dfrac{1}{n+1}\)