
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì x^2-2x+17<3-4x←→x^2+2x+14<0←→(x+1)^2+13<0←→Vô nghiệm
Ta có: \(x^2-2x+17< 3-4x\)
\(\Leftrightarrow x^2-2x+17-3+4x< 0\)
\(\Leftrightarrow x^2+2x+14< 0\)(1)
Ta có: \(x^2+2x+14\)
\(=x^2+2x+1+13\)
\(=\left(x+1\right)^2+13\)
Ta có: \(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+1\right)^2+13\ge13>0\forall x\)
hay \(x^2+2x+14>0\forall x\)(2)
Từ (1) và (2) suy ra \(x\in\varnothing\)
hay bất phương trình \(x^2-2x+17< 3-4x\) vô nghiệm(đpcm)

Ta có: |2x + 3| = 2x + 3 khi 2x + 3 ≥ 0 ⇔ x ≥ -1,5
|2x + 3| = -2x – 3 khi 2x + 3 < 0 ⇔ x < -1,5
Ta có: 2x + 3 = 2x + 2 ⇔ 0x = -1
Phương trình vô nghiệm.
-2x – 3 = 2x + 2
⇔ -2x - 2x = 2 + 3
⇔ -4x = 5
⇔ x = -1,25
Giá trị x = -1,25 không thỏa mãn điều kiện x < -1,5 nên loại.
Vậy phương trình đã cho vô nghiệm.

Ta có:
2x – 3 = 2(x – 3)
⇔ 2x – 3 = 2x – 6
⇔ 2x - 2x = 3 – 6
⇔ 0x = -3 (vô lí)
Vậy phương trình đã cho vô nghiệm

a) Thay x = 2 vào bất phương trình ta được: x2 = 22 = 4 > 0
Vậy x = 2 là một nghiệm của bất phương trình x2 > 0.
Thay x = -3 vào bất phương trình ta được x2 = (-3)2 = 9 > 0
Vậy x = -3 là một nghiệm của bất phương trình x2 > 0.
b) Với x = 0 ta có x2 = 02 = 0
⇒ x = 0 không phải nghiệm của bất phương trình x2 > 0.
Vậy không phải mọi giá trị của ẩn x đều là nghiệm của bất phương trình đã cho.

a) Ta có \(\left|x\right|\ge0\) nên |x| + 1 > 0 với mọi x. Do đó phương trình đã cho vô nghiệm.
b) Tương tự, phân tích \(x^2+2x+3=\left(x+1\right)^2+2>0\)


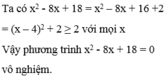
tham khảo câu hỏi của đắng sôcôla trên hoc24.vn nha