Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
+ Chuyển động tròn đều có tốc độ góc ω không đổI
+ Ta có ![]()
![]()
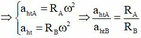
=20/15=4/3

\(\overrightarrow{F_D}+\overrightarrow{F_A}+\overrightarrow{F_B}=\overrightarrow{0}\Leftrightarrow F_D^2=F_A^2+F_B^2\)
\(\Leftrightarrow\left(\dfrac{G.m'.m\sqrt{2}}{AD^2}\right)^2=\left(\dfrac{G.m.m'}{AB^2}\right)^2+\left(\dfrac{G.m'.m}{AC^2}\right)^2\)
\(\Leftrightarrow\left(\dfrac{\sqrt{2}}{AD^2}\right)^2=\dfrac{1}{AB^4}+\dfrac{1}{AC^4}\Leftrightarrow\dfrac{2}{AD^2}=\dfrac{1}{a^4}+\dfrac{1}{a^4}=\dfrac{2}{a^4}\)
\(\Rightarrow AD=a^2\)
\(\overrightarrow{F_D}+\overrightarrow{F_A}+\overrightarrow{F_B}=\overrightarrow{0}\Leftrightarrow F_D^2=F_A^2+F_B^2\)
\(\Leftrightarrow\left(\dfrac{G.m'.m\sqrt{2}}{AD^2}\right)^2=\left(\dfrac{G.m.m'}{AB^2}\right)^2+\left(\dfrac{G.m'.m}{AC^2}\right)^2\)
\(\Leftrightarrow\left(\dfrac{\sqrt{2}}{AD^2}\right)^2=\dfrac{1}{AB^4}+\dfrac{1}{AC^4}\Leftrightarrow\dfrac{2}{AD^2}=\dfrac{1}{a^4}+\dfrac{1}{a^4}=\dfrac{2}{a^4}\)
\(\Rightarrow AD=a^2\)

Chọn D.
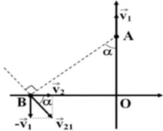
Xét hệ quy chiếu gắn với vật 1 thì vận tốc vật 2 đối với vật 1 là:
![]()
Tại thời điểm khoảng cách giữa hai vật nhỏ nhất thì v 21 → ⊥ A B
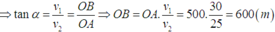

Chọn A.
Quỹ đạo của điểm A và B có án kính lần lượt là: rA = 20 cm, rB = 20 – 5 = 15 cm.
Hai điểm A, B có cùng tốc độ quay
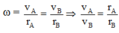
Tỉ số gia tốc:
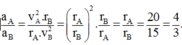

Chọn A.
Quỹ đạo của điểm A và B có án kính lần lượt là: r A = 20 cm, r B = 20 – 5 = 15 cm.
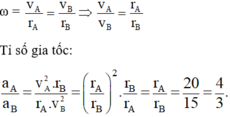
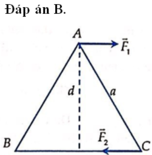


Đáp án D
Một vật phẳng mỏng đồng chất có dạng là một tam giác đều. Trọng tâm của vật đó nằm tại giao điểm của 3 đường trung tuyến (trong tam giác đều các đường trung tuyến, đường cao, đường phân giác, đường trung trực trùng nhau)→ D là phát biểu sai