Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
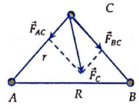
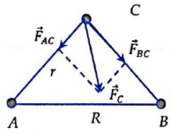
Vì tam giác ABC cân tại C nên ta có AC=BC= R 2
Lực hấp dẫn tác dụng lên chất điểm tại
![]()
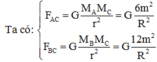
![]()

Lần sau tách câu hỏi ra cho dễ nhìn nhé
a/ Tìm M=?m
\(F_{hd1}=\dfrac{Gm_1m'}{r^2};F_{hd2}=\dfrac{Gm_2m'}{r^2};F_{hd3}=\dfrac{Gm_3m'}{r^2}\)
\(\sum\overrightarrow{F}=\overrightarrow{F_{hd1}}+\overrightarrow{F_{hd2}}+\overrightarrow{F_{hd3}}\)
\(\sum\overrightarrow{F}=\overrightarrow{0}\Rightarrow\overrightarrow{F_{hd1}}+\overrightarrow{F_{hd3}}=-\overrightarrow{F_{hd2}}\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{F_{hd13}}\uparrow\downarrow\overrightarrow{F_{hd2}}\left(t/m\right)\\F_{hd13}=F_{hd2}\end{matrix}\right.\)
\(\Rightarrow F_{hd13}=F_{hd2}\Leftrightarrow\sqrt{F_{hd1}^2+F_{hd3}^2+2F_{hd1}.F_{hd3}.\cos\left(\widehat{F_{hd1};F_{hd3}}\right)}=F_{hd2}\)
\(\Leftrightarrow\sqrt{F_{hd1}^2+F_{hd3}^2+2F_{hd1}.F_{hd3}.\cos120^0}=F_{hd2}\)
\(\Leftrightarrow\left(\dfrac{Gm_1m'}{r^2}\right)^2+\left(\dfrac{Gm_3m'}{r^2}\right)^2-\left(\dfrac{Gm_1m'}{r^2}\right).\left(\dfrac{Gm_3m'}{r^2}\right)=\left(\dfrac{Gm_2m'}{r^2}\right)^2\)
\(\Leftrightarrow m_1^2+m_3^2-m_1m_3=m_2^2\Leftrightarrow M^2+m^2-M.m=m^2\)
\(\Leftrightarrow M\left(M-m\right)=0\Leftrightarrow M=m\)

gọi khoảng cách từ m đến m1 là x
khoảng cách từ m đến m2 là 0,1-x
\(F_{hd1}=F_{hd2}\) và m1=9m2
\(\Rightarrow\)\(\dfrac{G.m.m_1}{x^2}=\dfrac{G.m.m_2}{\left(0,1-x\right)^2}\)\(\Rightarrow x=0,075\)m
vậy m cách m1 một khoảng x=0,075m

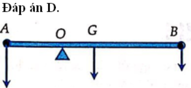
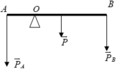
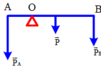
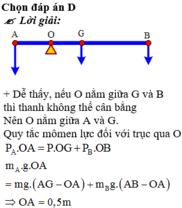
Dễ thấy, nếu O nằm giữa G và B thì thanh không thể cân bằng nên O nằm giữa A và G. Quy tắc mômen lực đối với trục qua O:
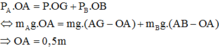

Ta có:
P = m g = 2.10 = 20 ( N ) ; P A = m A . g = 5.10 = 50 ( N ) ; P B = m B . g = 1.10 = 10 ( N )
Theo điều kiện cân bằng Momen lực: MA = MP + MB
⇒ P A . O A = P . O G + P B . O B
AG = GB = 1m
OG = AG – OA = 1 – OA
OB = AB – AO = 2 – OA
=> 50. OA = 20 (1- OA) + 10( 2 – OA )
=> OA = 0,5m


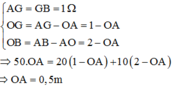
\(\overrightarrow{F_D}+\overrightarrow{F_A}+\overrightarrow{F_B}=\overrightarrow{0}\Leftrightarrow F_D^2=F_A^2+F_B^2\)
\(\Leftrightarrow\left(\dfrac{G.m'.m\sqrt{2}}{AD^2}\right)^2=\left(\dfrac{G.m.m'}{AB^2}\right)^2+\left(\dfrac{G.m'.m}{AC^2}\right)^2\)
\(\Leftrightarrow\left(\dfrac{\sqrt{2}}{AD^2}\right)^2=\dfrac{1}{AB^4}+\dfrac{1}{AC^4}\Leftrightarrow\dfrac{2}{AD^2}=\dfrac{1}{a^4}+\dfrac{1}{a^4}=\dfrac{2}{a^4}\)
\(\Rightarrow AD=a^2\)
\(\overrightarrow{F_D}+\overrightarrow{F_A}+\overrightarrow{F_B}=\overrightarrow{0}\Leftrightarrow F_D^2=F_A^2+F_B^2\)
\(\Leftrightarrow\left(\dfrac{G.m'.m\sqrt{2}}{AD^2}\right)^2=\left(\dfrac{G.m.m'}{AB^2}\right)^2+\left(\dfrac{G.m'.m}{AC^2}\right)^2\)
\(\Leftrightarrow\left(\dfrac{\sqrt{2}}{AD^2}\right)^2=\dfrac{1}{AB^4}+\dfrac{1}{AC^4}\Leftrightarrow\dfrac{2}{AD^2}=\dfrac{1}{a^4}+\dfrac{1}{a^4}=\dfrac{2}{a^4}\)
\(\Rightarrow AD=a^2\)