Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành

a) Xét tam giác ACD có: AF=FC (gt) ; DK=KC (gt)
=> FK là đường trung bình của tam giác ACD
=> FK//AD
=> ADKF là hình thang
Chứng minh tương tự t cũng có: ME là đường trung bình của tam giác ABD
=> ME // AD mà FK//AD (cmt)
=> ME//FK (1)
Chứng minh tương tự ta cũng có:
MF là đường trung bình tam giác ABC , EK là đường trung bình tam giác DBC
=> MF//BC ; EK // BC
=> MF//EK (2)
Từ (1) và (2) ta có: EMFK là hình bình hành

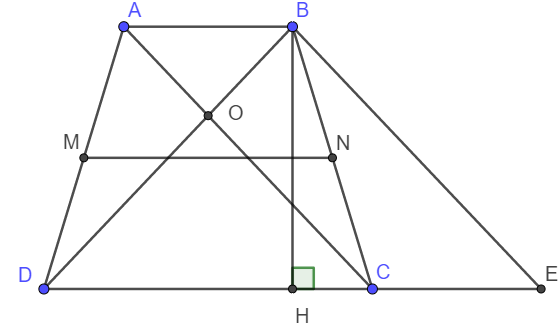
a) Xét tứ giác ABEC có AB // CE; AC // BE .
Vậy nên ABEC là hình bình hành. Suy ra AB = CE.
Do MN là đường trung bình hình thang ABCD nên ta có :
\(MN=\frac{AB+DC}{2}=\frac{CE+DC}{2}=\frac{DE}{2}.\)
b) Do ABCD là hình thang cân nên ta có:
\(AD=BC;DB=AC\)
Xét tam giác ABD và tam giác BAC có:
Cạnh AB chung
AD = BC
BD = AC
\(\Rightarrow\Delta ABD=\Delta BAC\left(c-c-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{BAC}\) hay \(\widehat{ABO}=\widehat{BAO}\)
Xét tam giác OAB có \(\widehat{ABO}=\widehat{BAO}\) nê OAB là tam giác cân tại O.
c) Do ABEC là hình bình hành nên AC = BE
Lại có AC = BD nên BD = BE
Suy ra tam giác BDE cân tại B.
Tam giác cân BDE có BH là đường cao nên đồng thời là đường trung tuyến.
Lại có theo câu a thì MN = DE/2
Giả thiết lại cho MN = BH. Vậy nên BH = DE/2
Xét tam giác BDE có trung tuyến BH bằng một nửa cạnh tướng ứng nên BDE là tam giác vuông tại B.
Vậy BDE là tam giác vuông cân tại B.

Bài 3:
Do chỉ sử dụng kiến thức chương I, nên cô giải như sau:
Gọi M là trung điểm BC. Kẻ MN // BK.
Lấy I, J là trung điểm của AG và HG.
Do BK và CL cùng vuông góc với KL nên BK // CL. Vậy KBCL là hình thang vuông.
Xét hình thang vuông KBCL là M là trung điểm BC, MN // BK nên MN là đường trung bình hình thang.
Suy ra 2MN = BK + CL
Xét tam giác AHG có I, J là các trung điểm của các cạnh AG và HG nên IJ là đường trung bình hay AH = 2IJ và \(IJ\perp KL\).
Xét tam giác ABC có G là trọng tâm nên GA = 2GM, vậy thì GI = GM.
Vậy thì \(\Delta GMN=\Delta GIJ\) (Cạnh huyền - góc nhọn)
Suy ra \(MN=IJ\Rightarrow2MN=2IJ\Rightarrow BK+CL=AH.\)
Bài 2:
Gọi I, J lần lượt là trung điểm AB và A'B'. Khi đó ta đã có I cố định.
Do d //d' nên AA'B'B là hình thang. Vậy thì IJ là đường trung bình hay \(IJ=\frac{AA'+BB'}{2}=\frac{AC+CB}{2}=\frac{AB}{2}\)
Ta thấy do AB không đổi nên độ dài AB là số không đổi, vậy AB/2 cũng không đổi.
Ta thấy J nằm trên tia Ix // d// d' mà độ dài đoạn IJ không đổi nên J là điểm cố định.
Tóm lại trung điểm của A'B' là điểm cố định thỏa mãn nằm trên tia Ix // d // d' và IJ = AB/2.
a: Xét ΔADC có
M là trung điểm của DA
E là trung điểm của DC
Do đó ME là đường trung bình
=>ME//AC và ME=AC/2(1)
Xét ΔBDC có
E là trung điểm của DC
N là trung điểm của BC
Do đó: EN là đường trung bình
=>EN=BD/2(2)
Từ (1) và (2) và AC=BD suy ra EM=EN
hay góc EMN=góc ENM
b: Gọi l là trung điểm của BD
Xét ΔDAB có
M là trung điểm của DA
I là trung điểm của DB
DO đó: MI là đường trung bình
=>MI//AB và MI=AB/2
Xét ΔBDC có
I là trung điểm của BD
N là trung điểm của bC
Do đó: IN là đường trung bình
=>IN//DC và IN=DC/2
=>MN<=(AB+CD)/2
c: Nếu MN=(AB+CD)/2 thìMN=MI+IN
=>M,I,N thẳng hàng
=>AB//CD