Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
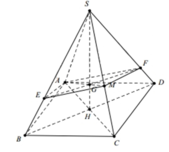
Gọi H là tâm của hình vuông A B C D ; S B H ^ = 60 0 ; H B = a 2 2
Khi đó là trọng tâm tam giác SAC.
Qua G dựng đường thẳng song song với BD cắt SB;SD lần lượt là E và F.
Do tính chất đối xứng ta có:
V S . A E M F V S . A B C D = V S . A E M V S . A B C = S E S B . S M S C = 2 3 . 1 2 = 1 3 .
Mặt khác V A . A B C D = 1 3 S H . S A B C D = 1 3 H B tan 60 0 . a 2 = a 3 6 6 .
Do đó V S . A E M F = 1 3 . a 3 6 6 = a 3 6 18 .

a: Xét ΔHAD vuông tại H và ΔABD vuông tại A có
\(\widehat{ADB}\) chung
Do đó: ΔHAD\(\sim\)ΔABD
b: BD=25cm
AH=12cm
c: XétΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\)
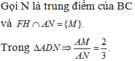
đặt
Ta có
mà
tới đây thế vào thôi
trường hợp có cạnh đối song song thì không tính được
Bài 2 mình làm trường hợp cả 2 đều là phân giác trong nhé
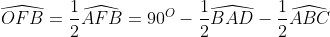
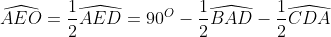
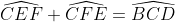
)
)
Gọi O là giao điểm của 2 đường phân giác trong kẻ từ E và F