Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
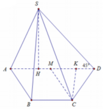
Gọi M là trung điểm cuả AD. Ta có: B C = A M = a và B C / / A M
nên tứ giác ABCM là hình bình hành
⇒ C M = A B = a ⇒ Δ C D M đều. Gọi K là hình chiếu của C lên AD.
Ta có: C K = a 2 − a 2 2 = a 3 2 .
Diện tích hình thang ABCD là: S = a + 2 a . a 3 2 2 = 3 a 2 3 4
+) Lại có:
H D = 3 2 .2 a = 3 a 2 ⇒ S H = 3 a 2
Thể tích khối chóp S.ABCD là:
V = 1 3 S H . S A B C D = 1 3 . 3 a 2 . 3 a 2 3 4 = 3 a 3 3 8 .

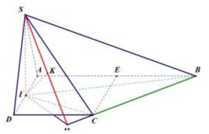
Gọi M; E là trung điểm của AI và CD
Kẻ S H ⊥ C D do mặt phẳng (SCD) vuông góc với mặt phẳng(ABCD) nên S H ⊥ A B C D . Mặt khác SA = SI
⇒ S M ⊥ A I ⇒ A I ⊥ S H M ⇒ H K ⊥ S A I
mà CD . Song song với S A B ⇒ H K là khoảng cách cần tìm. Qua E kẻ đường thẳng song song với BC cắt AB tại F
⇒ E F = a 13 4 ; F I = a 4 ⇒ H M = a 3 2 ⇒ H B = a 3 S H = H B . tan 30 o = a 3 . 1 3 = a
Ta có
1 H K 2 = 1 S H 2 + 1 H M 2 = 1 a 2 + 4 3 a 2 = 7 3 a 2 ⇒ H K = a 21 7
Đáp án cần chọn là D

Đáp án A
Phương pháp: Xác định góc giữa hai mặt phẳng bằng cách xác định góc giữa hai đường thẳng lần lượt vuông góc với giao tuyến.
Cách giải:
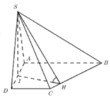
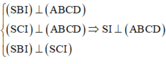
Kẻ IH
⊥
CD ta có: 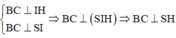
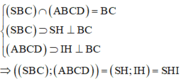
Ta có: 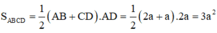
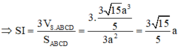
Gọi E là trung điểm của AB => EC = AD = 2a
![]()
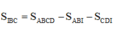
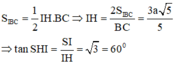




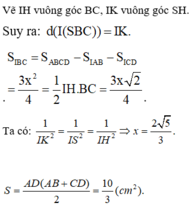



nhiều bài thế
Thế này chắc sáng mai chẳng xong mất