Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tg ABC vuông tại A
Áp dụng định lí Pitago ta có,
BC2=AC2+AB2, thay số
BC2= 82+62
BC2= 64+36
BC2= 100
BC2=102 \(\Rightarrow\)BC=10
b) Do DE vừa là đường cao vừa là đường trung tuyến nên tam giác DBC cân suy ra góc DBC bằng góc DCB

\(a,\)(Sửa đề: \(\Delta ABD=\Delta EBD\))
Vì \(\begin{cases} AB=BE\\ \widehat{ABD}=\widehat{EBD}\\ BD\text{ chung} \end{cases}\) nên \(\Delta ABD=\Delta EBD(c.g.c)\)
\(\Rightarrow \widehat{BAD}=\widehat{BED}=90^0\\ \Rightarrow DE\bot BC\)
\(b,\Delta ABD=\Delta EBD(cmt)\\ \Rightarrow AD=DE\Rightarrow D\in\text{trung trực }AE\\ AB=BE\Rightarrow B\in \text{trung trực }AE\\ \Rightarrow BD\text{ là trung trực }AE\)
\(c,\begin{cases} \widehat{MAD}=\widehat{CED}=90^0\\ AD=DE\\ AM=EC \end{cases}\\\Rightarrow \Delta ADM=\Delta EDC(c.g.c)\\ \Rightarrow MC=MD\)
\(d,\Delta ADM=\Delta EDC(cmt)\\ \Rightarrow \widehat{ADM}=\widehat{EDC}\)
Mà 2 góc này ở vị trí đối đỉnh và \(A,D,C\) thẳng hàng nên \(M,D,E\) thẳng hàng
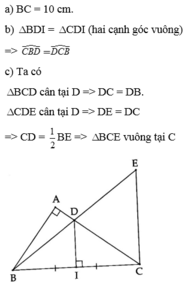
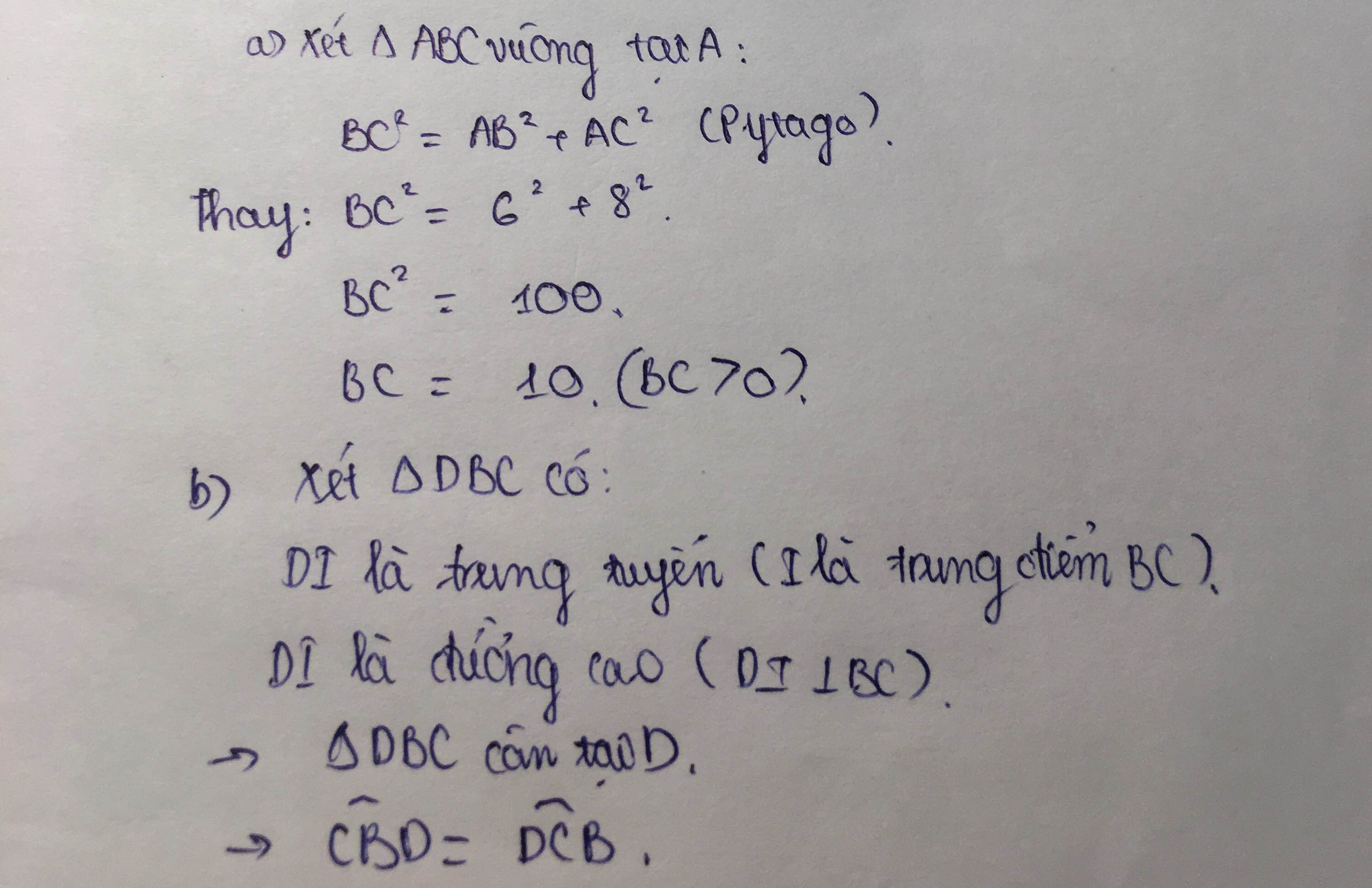
a) Áp dụng định lí Py Ta go cho tam giác ABC vuông tại A ta có:
BC2 = BA2 + CA2
= 62 + 82 = 100
Vậy BC = \(\sqrt{100}=10cm\)
b) Đặt Trung trực của BC cắt BC tại I
Xét tam giác BDI và tam giác CDI có:
ID chung
IB = IC
Góc BID = góc CID
Vậy tam giác BDI = tam giác CDI (c - g - c)
=> Góc DBC = DCB (2 góc tương ứng)
c. ta có tam giác ECD cân tại D => góc DEC= góc DCE = (180 - góc ADC): 2 (1)
ta lại có góc BDI + góc IDC + CDE = 180 độ
=> góc BDI + góc IDC = 180- góc CDE
mà theo câu b ta có Góc BDI= góc ICD
nên ta có góc BDI= góc IDC= (180- góc CDE):2 (2)
từ (1) và (2) => góc BDI = góc DEC mà 2 góc này ở vị trí đồng vị nên EC// DI
mà DI vuong góc với BC => EC vuông góc với BC nên tgiac BCE vuông