Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BEAD có
\(\widehat{BEA}+\widehat{BDA}=180^0\)
Do đó: BEAD là tứ giác nội tiếp
hay B,E,A,D cùng thuộc 1 đường tròn
Tâm O là trung điểm của AB
b: Xét tứ giác ADCF có
\(\widehat{ADC}+\widehat{AFC}=180^0\)
Do đó: ADCF là tứ giác nội tiếp
hay A,D,C,F cùng thuộc 1 đường tròn
Tâm I là trung điểm của AC

Có:\(BH=\dfrac{AH}{tan\alpha}\)
\(CH=\dfrac{AH}{tan\beta}\)
\(\Rightarrow BH+CH=AH\left(\dfrac{1}{tan\alpha}+\dfrac{1}{tan\beta}\right)\)
\(\Rightarrow a=AH\left(\dfrac{1}{tan\alpha}+\dfrac{1}{tan\beta}\right)\)
\(\Leftrightarrow AH=\dfrac{a}{\dfrac{1}{tan\alpha}+\dfrac{1}{tan\beta}}\)
Vậy...

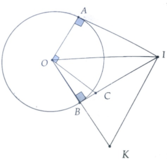
a, Chứng minh C là trực tâm của tam giác OIK. Từ đó suy ra KC ⊥ OI tại H
b, IA=12cm
Chứng minh ΔKOI cân tại K
Đặt KO = KI = x (x>0)
Có I K 2 = I B 2 + B K 2
Hay x 2 = 12 2 + x - 9 2
=> x = 12,5 => IK = 12,5cm

Xét ΔABC có \(BC^2=AB^2+AC^2\left(13^2=12^2+5^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot13=5\cdot12=60\)
hay \(AH=\dfrac{60}{13}\left(cm\right)\)
Cho mình sửa lại là IA=8cm chứ không phải 80cm nha :v mình nhầm