Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

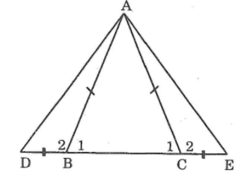
*) Ta có: ΔABC cân tại A

BD = CE (giả thiết)
Suy ra: ΔABD = ΔACE (c.g.c)
⇒ AD = AE ( hai cạnh tương ứng)
*) Tam giác ADE có AD = AE nên tam giác này cân tại A (theo định nghĩa tam giác cân)

Lời giải:
a) Xét tam giác $AHB$ và $AHC$ có:
$AH$ chung
$AB=AC$ do $ABC$ cân tại $A$
$\widehat{AHB}=\widehat{AHC}=90^0$
$\Rightarrow \triangle AHB=\triangle AHC$ (ch-cgv)
b)
Vì $ABC$ cân tại $A$ nên $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABD}=\widehat{ACE}$
Xét tam giác $ABD$ và $ACE$ có:
$BD=CE$
$AB=AC$
$\widehat{ABD}=\widehat{ACE}$ (cmt)
$\Rightarrow \triangle ABD=\triangle ACE$ (c.g.c)
$\Rightarrow AD=AE$ nên $ADE$ là tam giác cân.

a,xét tam giác ADB và AEC, ta có
AB=AC (gt) DB=CE(gt)
ABC=ACB=>ABD=ACE
=> tam giác ADB=AEC(c.g.c)
<=>AD=AE
=>ADE là tam giác cân
b, ta có ABC là tam giác cân
=>A=B=C=180/3=60
có góc ABD=180-60=120
=>DAB=ADB=(180-120)/2=30
góc EAC=DAB=30
<=>DAE=DAB+EAC+BAC=30+30+60=120

Giải:
a) Vì \(\Delta ABC\) có AB = AC nên \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{B_2}=\widehat{C_1}\)
\(\Rightarrow180^o-\widehat{B_2}=180^o-\widehat{C_1}\)
hay \(\widehat{DBE}-\widehat{B_2}=\widehat{ECD}-\widehat{C_1}\)
\(\Rightarrow\widehat{B_1}=\widehat{C_2}\) (*)
Xét \(\Delta ABD,\Delta ACE\) có:
\(AB=AC\left(gt\right)\)
\(\widehat{B_1}=\widehat{C_2}\) ( theo (*) )
\(BD=CE\left(gt\right)\)
\(\Rightarrow\Delta ABD=\Delta ACE\left(c-g-c\right)\)
\(\Rightarrow AD=AE\) ( cạnh t/ứng ) (đpcm)
b) Ta có: \(BM=MC\left(=\frac{1}{2}BC\right)\)
\(BD=CE\left(gt\right)\)
\(\Rightarrow BM+BD=MC+CE\)
\(\Rightarrow MD=ME\) (**)
Xét \(\Delta DAM,\Delta MAE\) có:
\(AD=AE\) ( theo phần a )
\(MD=ME\) ( theo (**) )
\(AM\): cạnh chung
\(\Rightarrow\Delta DAM=\Delta MAE\left(c-c-c\right)\)
\(\Rightarrow\widehat{DAM}=\widehat{MAE}\) ( góc t/ứng )
\(\Rightarrow AM\) là tia phân giác của \(\widehat{DAE}\left(đpcm\right)\)
Vậy...
Ta có hình vẽ
a/ Ta có: \(\widehat{ABC}\)=\(\widehat{ACB}\) (vì \(\Delta\)ABC cân) (*)
Mà \(\widehat{ABC}\)+\(\widehat{ABD}\)=1800 (kề bù) (**)
và \(\widehat{ACB}\)+\(\widehat{ACE}\)=1800 (kề bù) (***)
Từ (*),(**),(***) => \(\widehat{ABD}\) = \(\widehat{ACE}\) (1)
Ta có: AB = AC (GT) (2)
BD = CE (GT) (3)
Từ (1),(2),(3) => tam giác ABD = tam giác ACE
=> AD = AE (2 cạnh tương ứng) (đpcm)
b/ Xét tam giác AMD và tam giác AME có:
AD = AE (đã chứng minh ở câu a)
AM: cạnh chung
\(\begin{cases}BM=MC\\BD=CE\end{cases}\)\(\Rightarrow\) MB+BD=MC+CE \(\Rightarrow\)MD = ME
=> tam giác AMD = tam giác AME (c.c.c)
=> \(\widehat{DAM}\)=\(\widehat{EAM}\) (2 góc tương ứng)
=> AM là phân giác góc DAE (đpcm)

GT : Tam giác đều ABC
BD = CE = BC
KL Tam giác ADE là tam giác gì vì sao
Số đo góc DAE
CM:
a)Tam giác ABC là tam giác đều
Suy ra : \(\widehat{A_1}=\widehat{B_1}=\widehat{C_1}\)
AB=BC=AC
Vì \(\widehat{B_1}=\widehat{C_1}\) (chúng minh trên)
Suy ra : \(\widehat{B_2}=\widehat{C_{ }_2}\) (hai hóc kề bù)
\(\Delta ABD\) VÀ \(\widehat{ACE}\) CÓ:
AB = AC ( chứng minh trên)
\(\widehat{B_2}=\widehat{C_{ }_2}\) (CHỨNG MINH TRÊN )
BD = CE (GT)
Do đó : \(\Delta ABD=\Delta ACE\) (c. g. c)
Suy ra : \(\widehat{D}=\widehat{E}\)
=> \(\Delta ADE\) cân tại A
b)

a) Vì Góc B1+B2=180 độ(2 góc kè bù)
Góc C1+C2=180 độ( 2 góc kề bù)
mà: Góc B1=C1( tam giác ABC là tam giác đều)
=>Góc B2=C2
Xét tam giác ABD và tam giác ACE, có:
AB=AC( tam giác ABC là tam giác đều)
Góc B2=C2( cmt)
BD=CE( gt)
=> Tam giác ABD= tam giác ACE(c-g-c)
=>Góc D= góc E( 2 góc tương ứng)
=> Tam giác ADE là tam giác cân tại A.
Chúc các bạn học tốt nhaa!

Hình vẽ:
Giải:
Vì tam giác \(ABC\) cân tại \(A\):
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\) ( góc bù )
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(AB=AC \) \(\left(gt\right)\)
\(\widehat{ABD}=\widehat{ACE}\) \(\left(cmt\right)\)
\(BD=CE \) \(\left(gt\right)\)
Do đó: \(\Delta ABD=\Delta ACE\) \(\left(c.g.c\right)\)
\(\Rightarrow AD=AE\) ( cặp cạnh tương ứng )
\(\Rightarrow\Delta ADE\) cân tại \(A\).
Bài làm
Bạn tự vẽ hình nhé
Vì tam giác ABCABC cân tại A:
⇒ˆABC=ˆACB⇒ABC^=ACB^
⇒ˆABD=ˆACE⇒ABD^=ACE^ ( góc bù )
Xét ΔABDΔABD và ΔACEΔACE có:
AB=ACAB=AC (gt)
ˆABD=ˆACEABD^=ACE^ (cmt)
BD=CEBD=CE (gt)(gt)
Do đó: ΔABD=ΔACEΔABD=ΔACE (c.g.c)(c.g.c)
⇒AD=AE⇒AD=AE ( cặp cạnh tương ứng )
⇒ΔADE⇒ΔADE cân tại A

a)
b) Ta có : \(\left\{{}\begin{matrix}BC=AC\left(\Delta ABCđều\right)\\BC=CE\left(gt\right)\end{matrix}\right.\)
Suy ra : \(AC=CE\left(=BC\right)\)
Xét \(\Delta ACE\) có :
\(AC=EC\left(cmt\right)\)
=> \(\Delta ACE\) cân tại C
=> \(\widehat{CAE}=\widehat{CEA}\) (tính chất tam giác cân)
Ta có : \(\widehat{ACB}+\widehat{ACE}=180^o\) (kề bù)
=> \(60^o+\widehat{ACE}=180^o\)
=> \(\widehat{ACE}=180^o-60^o=120^o\)
Lại có : \(\widehat{CAE}=\widehat{CEA}=\dfrac{180^o-\widehat{ACE}}{2}\) (tổng 3 góc của 1 tam giác)
=> \(\widehat{CAE}=\widehat{CEA}=\dfrac{180^o-120^o}{2}=30^o\)
Chứng minh tương tự với \(\Delta ABD\) ta có :
\(\widehat{BDA}=\widehat{BAD}=\dfrac{180^{^O}-\widehat{ABD}}{2}\) (tổng 3 góc của 1 tam giác)
=> \(\widehat{BDA}=\widehat{BAD}=\dfrac{180^{^O}-120^{^O}}{2}=30^{^O}\)
Có : \(\widehat{DAE}=\widehat{BAD}+\widehat{BAC}+\widehat{CAE}\)
=> \(\widehat{DAE}=30^o+60^o+30^o=120^o\)
Lời giải:
a)
Tam giác $ABC$ đều nên \(AB=AC\) và \(\angle ABC=\angle ACB\)
\(\Leftrightarrow 180^0-\angle ABC=180^0-\angle ACB\)
\(\Leftrightarrow \angle DBA=\angle ECA\)
Xét tam giác $DBA$ và $ECA$ có:
\(\left\{\begin{matrix} \angle DBA=\angle ECA\\ BA=CA\\ DB=EC(=BC)\end{matrix}\right.\) \(\Rightarrow \triangle DBA=\triangle ECA(c.g.c)\)
\(\Rightarrow DA=EA\Rightarrow \triangle ADE\) là tam giác cân.
Ta có đpcm.
b)
Có \(BD=BC\). Mà \(AB=BC\) (do tam giác đều)
\(\Rightarrow BD=AB\)
Do đó tam giác $DBA$ cân tại $B$
\(\Rightarrow \angle BAD=\angle BDA\)
Mà: \(\angle BAD+\angle BDA=\angle ABC=60^0\) (do tam giác $ABC$ đều)
Suy ra \(\angle BAD=\angle BDA=\frac{60^0}{2}=30^0\)
Theo phần a \(\triangle DBA=\triangle ECA\Rightarrow \angle BAD=\angle CAE=30^0\)
Do đó:
\(\angle DAE=\angle BAD+\angle BAC+\angle CAE=30^0+60^0+30^0=120^0\)