Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔBAC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(cạnh huyền-cạnh góc vuông)
Suy ra: BH=HC(hai cạnh tương ứng)

1: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
hay H là trung điểm của BC
2: BH=CH=BC/2=6cm
=>AH=8cm
3: Xét ΔAHE có
AK là đường cao
AK là đường trung tuyến
Do đó:ΔAHE cân tại A
hay AH=AE(1)
4: Xét ΔADH có
AI là đường cao
AI là đường trung tuyến
Do đó:ΔADH cân tại A
=>AD=AH(2)
Từ (1) và (2)suy ra AD=AE
hay ΔADE cân tại A

a: ΔAHB vuông tại H
=>AH<AB
b: Xét ΔKAD vuông tại K và ΔHBA vuông tại H có
AD=BA
góc KAD=góc HBA
=>ΔKAD=ΔHBA
=>KD=HB và AK=BH

ta có vì ABC vuông tại A suy ra \(BC^2=AB^2+AC^2\)(định lý pitago)
BC=10 suy ra \(BC^2=100\)
mà theo đề bài \(\frac{AB}{AC}=\frac{3}{4}\Rightarrow\frac{AB^2}{AC^2}=\frac{3^2}{4^2}=\frac{9}{16}\)
áp dụng tính chất tỉ lệ thức
\(\frac{AB^2}{AC^2}=\frac{9}{16}\Leftrightarrow\frac{AB^2}{9}=\frac{AC^2}{16}\)
áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{AB^2}{9}=\frac{AC^2}{16}=\frac{AB^2+AC^2}{9+16}=\frac{100}{25}=4\) \(\left(AB^2+AC^2=BC^2=100\right)\)
suy ra \(\frac{AB^2}{9}=4\Rightarrow AB^2=4.9=36\Rightarrow AB=6\)
suy ra\(\frac{AC^2}{16}=4\Rightarrow AC^2=4.16=64\Rightarrow AC=8\)

mk nghĩ bn áp dung t/c dãy tỉ số bằng nhau
ko bít được ko nhỉ??????????????

Ta có BC^2=AC^2+AB^2
Mà AB:AC=3:4
=>\(\frac{AB}{3}=\frac{AC}{4}=\frac{AB+AC}{3+4}=\frac{AC^2+AB^2}{3^2+4^2}=\frac{BC^2}{25}=\frac{100}{25}=4\)
=> AB^2=4*9=36=>AB=6cm
AC^2=4*16=67=>AC=8cm
Vậy chu vi tam giác ABC là 10+6+8=24 cm
ÁP dụng dịnh lí pytago ta có
BC2=102=100
=>AB2+AC2=100
áp dung dãy tỉ số = nhau
AB/3 = AC/4
AB2 / 9 =AC2/16
AB2+AC2/25 =100/25=4
=>AB/3=4 =>AB=12
AC/4 =4 =>AC=16
vậy chu vi tam giác ABC
10+12+16=38(cm)
ĐS:38cm

a, Theo định lí Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=\sqrt{64+36}=10\)cm
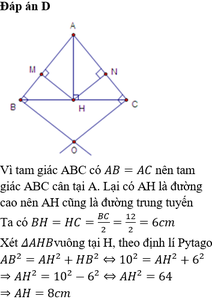
Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A
mà AH là đường cao đồng thời là đường trung tuyến
=> HC = HB = 6 cm
b, Vì tam giác ABC cân tại A => ^ABC = ^ACB
c, Vì tam giác ABC cân tại A, AH đồng thời là đường phân giác
=> ^BAH = ^HAC
Xét tam giác AMH và tam giác ANH có :
^AMH = ^ANH = 900
AH _ chung
^BAH = ^NAH ( cmt )
Vậy tam giác AMH = tam giác ANH ( ch - gn )
=> MH = NH ( 2 cạnh tương ứng )
Xét tam giác HMN có MH = NH ( cmt )
=> tam giác HMN cân tại H
chắc đúng ko đấy bn đây là bài kiểm tra nên tui phải làm đúng