Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\text{a) Có }\Delta ABC\text{cân tại A}\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\text{Xét }\Delta AHB\text{ và }\Delta AHC\text{ có:}\)
\(\widehat{AHB}=\widehat{AHC}=90^o\)
\(AB=AC=10cm\)\(\Rightarrow\)\( \Delta AHB\text{=}\Delta AHC\left(ch-gn\right)\)
\(\widehat{ABC}=\widehat{ACB}\)
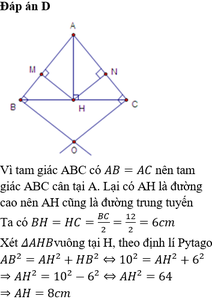
\(\text{b) Có }\Delta AHB=\Delta AHC\Rightarrow HB=HC=\frac{BC}{2}=\frac{12}{2}=6\left(cm\right)\)
\(\text{ Xét }\Delta AHB\text{vuông tại H có:}\)
\(AH^2+BH^2=AB^2\) (Định lý py-ta-go)
\(AH^2=AB^2-BH^2=10^2-6^2=100-36=64\)
\(AH=\sqrt{64}=8\left(cm\right)\)
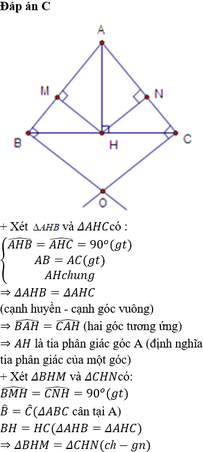
\(\text{c) Xét }\Delta BHM\text{ và }\Delta CHN\text{ có:}\)
\(\widehat{BMH}=\widehat{CNH}=90^o\)
\(HB=HC\text{ (CMT)}\)\(\Rightarrow\)\(\text{ }\Delta BHM\text{ = }\Delta CHN \left(CH-GN\right)\)
\(\widehat{ABC}=\widehat{ACB}\)
\(\text{d) }\)\(\text{Ta có: }MH\perp AB,OB\perp AB\Rightarrow MH//OB\)
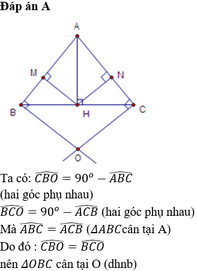
\(\Rightarrow\widehat{MHB}=\widehat{CBO}\text{ (2 góc so le trong)}\)
\(\text{Ta có: }NH\perp AC,OC\perp AC\Rightarrow NH//OC\)
\(\Rightarrow\widehat{NHC}=\widehat{BCO}\text{ (2 góc so le trong)}\)
\(\text{ }\text{Mà }\Delta BHM\text{ = }\Delta CHN\Rightarrow\widehat{MHB}=\widehat{NHC}\)
\(\text{Hay}\widehat{CBO}=\widehat{BCO}\)\(\Rightarrow\Delta OBC\text{ cân tại O}\)

â)Ta có : AB = AC =10 cm (gt)
=> tam giác ABC cân tại A (2 cạnh bên = nhau )
b) Xét tam giác AHB va tam giac AHC ,co :
\(\widehat{AHB}=\widehat{AHC}=90^O\) ( AH là đường cao )
AB =AC =10 cm (gt )
AH là cạnh chung
Do đo : tam giác AHB =tam giác AHC ( cạnh huyền - cạnh góc vuông )
=>\(\widehat{BAH}=\widehat{CAH}\)( hai góc tương ứng )
=>AH là tia phân giác của góc A
c)Vì trong tam giác cân đường phân giác đồng thời là đường trung tuyến của tam giác
Nên :H là trung điểm của BC
=>BH = CH = \(\frac{BC}{2}\)=12/2 = 6 cm
TRẢ LỜI TIẾP CÂU Ở TRÊN NHA ( HỒI NÃY BẤM NHẦM GỬI TRẢ LỜI )
b) Vì trong tam giác cân đường phân giác đồng thời là đường trung tuyến của tam giác
Nên : H là trung điểm của BC
=> BH =CH =\(\frac{BC}{2}=\frac{12}{2}=6cm\)
Xét : tam giác BMH và tam giác HCN , co :
BH = CH = 6cm ( chứng minh trên )
\(\widehat{M}=\widehat{N}=90^o\left(gt\right)\)
\(\widehat{B}=\widehat{C}\) (Vì tam giác ABC cân tại A nên hai góc ở đáy = nhau )
Do do:tm giác BHM = tam giác HCN
đ) Áp dụng định lý pytago vào tam giác AHC vuông tại H
\(AH^2=AC^2-HC^2\) =\(10^2-6^2\)=\(100-36=64\)
=>\(AH=\sqrt{64}=8cm\) OK CHÚC BẠN HỌC TỐT

1.a)
Vì AB=AC => Tam giác ABC cân
b)
Vì △ABC cân
=> góc ABC=góc ACB (1)
góc AHC=góc AHB=90 độ (2)
AB=AC (gt) (3)
Từ (1)(2)(3) => △AHB = △AHC (cạnh huyền-góc nhọn)
=> góc BAH = góc CAH
=> AH là tia phân giác của góc A
c) Vì góc ABC = góc ACB
=> góc MBH = góc NCH
góc BMH = góc HNC =90 độ
=> △BHM = △HCN (g.g)
d) Ta có: AH.BC=AB.AC
=> AH.12=10.10
=> AH = 25/3 (cm)