Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có I là trung điểm AC
Nên OI vuông góc AC (quan hệ đường kính và dây)
Do đó \(\widehat{OID}=90độ\)
Mà \(\widehat{OBD}=90độ\)(tính chất tiếp tuyến)
Suy ra\(\widehat{OID}+\widehat{OBD}=180độ\)
Vậy tứ giác OBDI nội tiếp (tổng 2 góc đối của tứ giác bằng 180 độ)
b) Ta có \(\widehat{ACB}=90độ\)(góc nội tiếp chắn nửa đường tròn)
Xét 2 tam giác vuông IBC và ODB có
\(\widehat{BIC}=\widehat{DOB}\)(tứ giác OBDI nội tiếp)
Nên ΔIBC ~ ΔODB
Do đó \(\frac{IB}{OD}\)=\(\frac{BC}{DB}\)
Hay IB.DB = OD.BC

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay ΔABC cân tại A
mà \(\widehat{BAC}=60^0\)
nên ΔABC đều

Chọn đáp án D
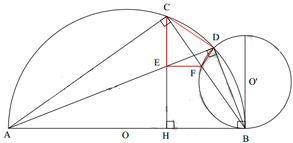

* Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B.
Đường tròn (O’) cắt CB tại F khác B. Chứng minh E F / / A B .
Ta có:

Hai góc ở vị trí đồng vị ⇒ E F / / A B
Chọn đáp án C.