Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta\)vuông ABC có \(AB^2+AC^2=BC^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{40^2-32^2}=24\left(cm\right)\)
Có E thuộc BC, BE=\(\frac{1}{2}\)BC (vì \(\frac{BE}{BC}=\frac{20}{40}=\frac{1}{2}\))
\(\Rightarrow E\)là trung điểm BC
Lại có \(\Delta ABC\)vuông tại A nên \(AB\perp AC\)
Mà \(EH\perp AB\)\(\Rightarrow EH//AC\)
Xét \(\Delta ABC\)có E là trung điểm BC; \(EH//AC\)
\(\Rightarrow\)HE là đường TB của \(\Delta ABC\)
\(\Rightarrow HE=\frac{1}{2}AC=\frac{24}{2}=12\left(cm\right)\)

a) Ta chứng minh:
S A E F = S A B C D = 1 4 S A B F
b) Từ câu a suy ra EH = CK
c) Gọi SBDE = S1; SADE = S2;
Ta chứng minh DE = DC;
Ta tính được:
ABDC = S1; SADC = S2, suy ra SABC = 2(S1 + S2) = 2.SABD
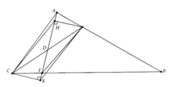

a) Ta có: AB = AE + EB ; AC = AF+ FC
mà AB = AC (gt); EB = CF (gt)
=> AE = AF => t/giác AEF cân tại A
=> \(\widehat{AEF}=\widehat{AFE}=\frac{180^0-\widehat{A}}{2}\) (1)
T/giác ABC cân tại A => \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AEF}=\widehat{B}\) mà 2 góc này ở vị trí đồng vị
=> EF // BC => tứ giác EFCB là hình thang có \(\widehat{B}=\widehat{C}\)
=> BEFC là hình thang cân
b) Ta có: \(\widehat{AFE\:}=\widehat{AEF}=\frac{180^0-\widehat{A}}{2}=\frac{180^0-40^0}{2}=70^0\)
\(\widehat{AFE\:}+\widehat{EFC\:}=180^0\) (kề bù) => \(\widehat{EFC\:}=180^0-\widehat{AFE\:}=180^0-70^0=110^0\)
c) Kẻ FG vuông góc với BC
Ta có: EF // BC (cmt)
EH \(\perp\)BC (gt)
=> HE \(\perp\)EF
Xét tứ giác EFGH có \(\widehat{HEF}=\widehat{EHG}=\widehat{HGF}=90^0\)
=> EFGH là HCN => EH = FG = 5 cm
St/giác BFC = 5.10/2 = 25 (cm2)

a) tam giác BAC vuông tại A và tam giác BMN vuong tại M có: góc BAC=góc BMN
=> tam giác BAC đồng dạng tam giác BMN (g-g)
=> BA/BM=BC/BN=> BN=BM.BC/BA=18.20/12=30cm
b) tam giác PAN vuong tại A và tam giác PMC vuong tại M có
góc APN=góc MPC (đối đỉnh)
=> tam giác PAN đồng dạng tam giác PMC (g-g)
=> PA/PM=PN/PC
=> PA.PC=PM.PN (đpcm)
c) xét tam giác BNC có MN và AC là hai đường cao cắt nhau tại P
=> BP là đường cao thứ 3 kẻ từ B
=> BP vuong góc NC (đpcm)
Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=24cm\)
Vì EH vuông BA ; CA vuông BA => CA // EH ( tc vuông góc tới song song )
Theo hệ quả Ta lét \(\frac{BE}{BC}=\frac{EH}{AC}\Rightarrow EH=\frac{BE.AC}{BC}=12cm\)