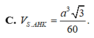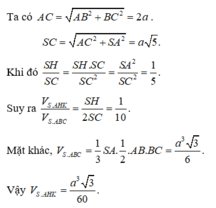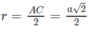Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

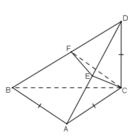
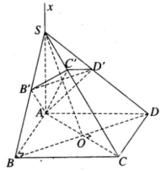
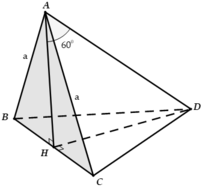
gọi (α) là mặt phẳng qua C vuông góc với BD
tam giác ABC vuông cân ở A và AB= a => BC = a√2
tam giác ACD vuông cân ở C và AC = a => AD = a√2
BD^2 = CD^2 + BC^2 = a^2 + 2a^2 = 3a^2 => BD = a√3
BD L (α) => BD L CF
DC L (ABC) => DC L BC
ta có:
CD^2 = DF.BD => DF = CD^2/BD = a^2/(a√3) = a/√3
BD L (α) => BD L EF
DC L (ABC) và AB L AC => AB L AD ( định lý 3 đường vuông góc)
=> ΔDEF ~ Δ DBA => DF/DA = DE/BD
=> DE = DF.BD/DA = (a/√3)(a√3)/(a√2) = a/√2
V = V(DABC) = S(ABC).CD/3 = (a^2/2).a/3 = a^3/6
V1 = V(CDEF) = V(DCEF)
ta có:
V1/V = (DC/DC).(DE/DA).(DF/DB) = 1.[(a/√2)/(a√2)].[(a/√3)/(a√3)] = 1/6
=> V1 = V/6 = (a^3/36)

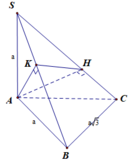
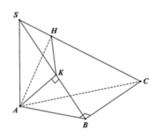
\(BC=AB\sqrt{2}=a\sqrt{2}\)
\(SB=\sqrt{SC^2+BC^2}=a\sqrt{3}\) ; \(SA=\sqrt{SC^2+AC^2}=a\sqrt{2}\)
\(V_{SBAC}=\dfrac{1}{3}SC.\dfrac{1}{2}AB^2=\dfrac{a^3}{6}\)
\(\dfrac{V_{SCEF}}{V_{SABC}}=\dfrac{SF}{SB}.\dfrac{SE}{SA}=\left(\dfrac{SC}{SB}\right)^2\left(\dfrac{SC}{SA}\right)^2=\left(\dfrac{a}{a\sqrt{3}}\right)^2.\left(\dfrac{a}{a\sqrt{2}}\right)^2=\dfrac{1}{6}\)
\(\Rightarrow V_{SCEF}=\dfrac{1}{6}.\dfrac{a^3}{6}=\dfrac{a^3}{36}\)
Kết quả không có a³/18
Chỉ có là A)a³/6. B)a³/16
C)a³/26. D)a³/36 thôi ạ

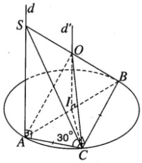
Trường hợp mặt phẳng (SBC) tạo với mặt phẳng (ABC) một góc 30 ° thì góc của hai mặt phẳng đó chính là góc ∠ SCA. Thực vậy vì SA ⊥ (ABC) mà AC ⊥ CB nên ta có SC ⊥ CB. Do đó ∠SCA = 30 ° .
Vì AB = 2a nên ta có AC = a 2 ta suy ra
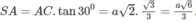
Gọi r là bán kính mặt cầu ngoại tiếp tứ diện khi ∠ SCA = 30 °
Ta có r = SB/2 = OA = OB = OC = OS, trong đó SB 2 = SA 2 + AB 2
Vậy
![]()
Do đó 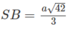
Ta suy ra 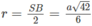

Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với (ABC) \(\Rightarrow SA\perp\left(ABC\right)\)
\(AB\perp BC\Rightarrow SB\perp BC\Rightarrow\widehat{SBA}\) là góc giữa 2 mặt phẳng (SBC) và mặt phẳng (ABC)
\(\Rightarrow\widehat{SBA}=60^o\)
\(\Rightarrow SA=AB.\tan\widehat{SBA}=2a\sqrt{3}\)
Mặt phẳng qua SM và song song với BC, cắt AC tại N
\(\Rightarrow MN||BC\) và N là trung điểm của \(AC\\ \)
\(MN=\frac{BC}{2}=a;BM=\frac{AB}{2}=a\)
Diện tích \(S_{BCNM}=\frac{\left(BC+MN\right).BM}{2}=\frac{3a^2}{2}\)
Thể tích \(V_{S.BCNM}=\frac{1}{3}S_{BCNM}.SA=a^3\sqrt{3}\)
Kẻ đường thẳng \(\Delta\) đi qua N, song song với AB
Hạ \(AD\perp\Delta\left(D\in\Delta\right)\Rightarrow AB||\left(SND\right)\)
\(\Rightarrow d\left(AB;SN\right)=d\left(AB,\left(SND\right)\right)=d\left(A,\left(SND\right)\right)\)
Hạ \(AH\perp SD\left(H\in SD\right)\Rightarrow AH\perp\left(SND\right)\Rightarrow d\left(A,\left(SND\right)\right)=AH\)
Tam giác SAD vuông tại A : \(\begin{cases}AH\perp SD\\AD=MN=a\end{cases}\)
\(\Rightarrow d\left(AB,SN\right)=AH=\frac{SA.AD}{\sqrt{SA^2+AD^2}}=\frac{2a\sqrt{39}}{13}\)

Đáp án C
Ta có
![]()
![]()
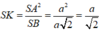
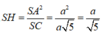
V S . A H K V S . A B C = S K . S H S B . S C = 1 10
⇒ V S . A H K = 1 10 V S . A B C = 1 60 3 a 3