Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(SA\perp BC\), \(AB\perp BC\) \(\Rightarrow SB\perp BC\)
Do đó : góc giữa 2 mặt phẳng (SBC) và (ABC) bằng \(\widehat{SBA}=30^0\)
\(V_{S.ABM}=\frac{1}{2}V_{S.ABC}=\frac{1}{2}SA.AB.BC\)
\(BC=AB=a;SA=AB.\tan30^0=\frac{a\sqrt{3}}{3}\)
Vậy \(V_{s.ABM}=\frac{a^3\sqrt{3}}{36}\)

1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.

Kẻ SH vuông góc với BC tại H => SH vuông góc với (ABC)
Kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N
Ta có góc SMH = góc SNH = 60 độ
Dễ thấy tam giác SHM = tam giác SHN => HM = HN
Ta có HM = HB.sin 30 = 1/2 HB hay HB = 2 HM
HN = HC.sin 60 = HC.căn 3 /2 => HC = 2/căn 3.HN = 2/căn 3 .HM
=> BC = a = HB + HC = ( 2 + 2/căn 3).HM
=> HM = a/(2 + 2/căn 3) = a.căn 3 /(2+ 2.căn 3)
=> SH = HM.tan 60 = 3a/(2+2.căn 3)
Có AB = BC/2 = a/2
AC = BC.căn 3/2 = a.căn 3/2
S(ABC) = 1/2.AB.AC = 1/8.a^2.căn 3
=> V(SABC) = 1/3.3a/(2+2.căn 3) . 1/8.a^2.căn 3 = a^3.căn 3 /[16.(1+ căn 3)]

Chọn A
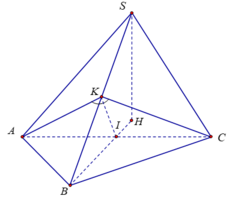
Cách 1:
Dễ thấy hai tam giác SAB và SAC bằng nhau (cạnh chung SA), gọi K là chân đường cao hạ từ A trong tam giác SAB
![]()
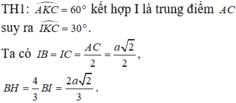
Từ giả thiết tam giác ABC vuông cân tại B ta được ![]()
Trong tam giác ICK vuông tại I có 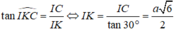 .
.
Như vậy Ik > IB (vô lý).
TH2: ![]() tương tự phần trên ta có
tương tự phần trên ta có 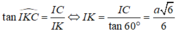
Do ![]() nên tam giác BIK vuông tại K và
nên tam giác BIK vuông tại K và 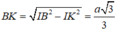
Như vậy tam giác BKI đồng dạng với tam giác BHS suy ra: ![]()
Vậy thể tích của khối chóp S.ABC là 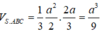
Cách 2: dùng phương pháp tọa độ hóa.
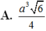
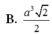
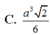
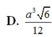

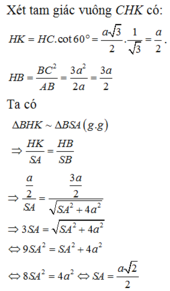
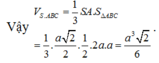
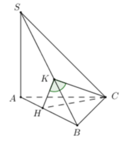


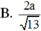

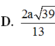

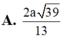
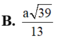
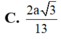
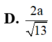

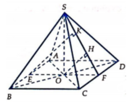
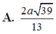
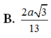
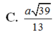
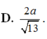


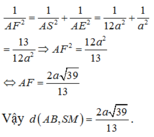
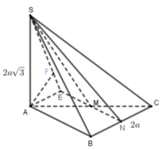
Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với (ABC) \(\Rightarrow SA\perp\left(ABC\right)\)
\(AB\perp BC\Rightarrow SB\perp BC\Rightarrow\widehat{SBA}\) là góc giữa 2 mặt phẳng (SBC) và mặt phẳng (ABC)
\(\Rightarrow\widehat{SBA}=60^o\)
\(\Rightarrow SA=AB.\tan\widehat{SBA}=2a\sqrt{3}\)
Mặt phẳng qua SM và song song với BC, cắt AC tại N
\(\Rightarrow MN||BC\) và N là trung điểm của \(AC\\ \)
\(MN=\frac{BC}{2}=a;BM=\frac{AB}{2}=a\)
Diện tích \(S_{BCNM}=\frac{\left(BC+MN\right).BM}{2}=\frac{3a^2}{2}\)
Thể tích \(V_{S.BCNM}=\frac{1}{3}S_{BCNM}.SA=a^3\sqrt{3}\)
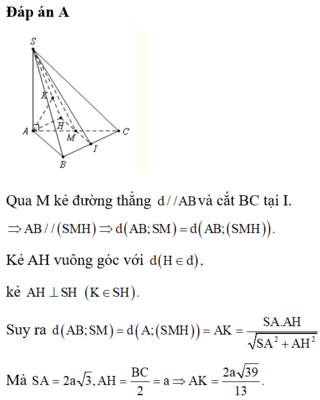
Kẻ đường thẳng \(\Delta\) đi qua N, song song với AB
Hạ \(AD\perp\Delta\left(D\in\Delta\right)\Rightarrow AB||\left(SND\right)\)
\(\Rightarrow d\left(AB;SN\right)=d\left(AB,\left(SND\right)\right)=d\left(A,\left(SND\right)\right)\)
Hạ \(AH\perp SD\left(H\in SD\right)\Rightarrow AH\perp\left(SND\right)\Rightarrow d\left(A,\left(SND\right)\right)=AH\)
Tam giác SAD vuông tại A : \(\begin{cases}AH\perp SD\\AD=MN=a\end{cases}\)
\(\Rightarrow d\left(AB,SN\right)=AH=\frac{SA.AD}{\sqrt{SA^2+AD^2}}=\frac{2a\sqrt{39}}{13}\)
1242