Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{ADC}\)(Hệ quả góc nội tiếp)
hay \(\widehat{ABH}=\widehat{ADC}\)(1)
Xét (O) có
ΔADC nội tiếp đường tròn(A,D,C∈(O))
AD là đường kính(gt)
Do đó: ΔADC vuông tại C(Định lí)
Suy ra: \(\widehat{DAC}+\widehat{ADC}=90^0\)(Hai góc nhọn phụ nhau)(2)
Ta có: ΔABH vuông tại H(AH⊥BC)
nên \(\widehat{BAH}+\widehat{ABH}=90^0\)(Hai góc nhọn phụ nhau)(2)
Từ (1) và (2) suy ra \(\widehat{BAH}=\widehat{DAC}\)(đpcm)

Vẽ đường kính AK
+) Dễ có: ^KBC = ^KAC (2 góc nội tiếp cùng chắn cung KC) (1)
+) ^ABK là góc nội tiếp chắn nửa đường tròn nên ^ABK = 900
Có: ^KBC + ^CBA = ^ABK = 900 (cmt)
^BAH + ^CBA = 900 (∆ABH vuông tại H)
Từ đó suy ra ^KBC = ^BAH (2)
Từ (1) và (2) suy ra ^BAH = ^KAC hay ^BAH = ^OAC (đpcm)
Kẻ đường kính AE của đường tròn ( O) . Ta thấy \(\widehat{ACE}=90^o\)( góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow\widehat{OAC}+\widehat{AEC}=90^o\) (1)
Theo gt, ta có: \(\widehat{BAH}+\widehat{ABC}=90^O\) (2)
Lại có: \(\widehat{AEC}=\widehat{ABC}\) (3)
Từ (1), (2), (3) => đpcm

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
góc EAH+góc ACB=90 độ
góc EBC+góc ACB=90 độ
=>góc EAH=góc EBC
b: AK cắt EF tại M
AK cắt BC tại N
AH cắt (O) tại K
=>HM//AB và QN//AB
=>HM//QN

a) Ta có: AM là phân giác \(\widehat{BAC}\)=> \(\widehat{BAM}\)= \(\widehat{CAM}\)=> \(\widebat{BM}\)=\(\widebat{CM}\)
=> BM = CM
mà OB=OC (bán kính (O))
=> OM là đường trung trực của BC => OM đi qua tđ N của BC
b) Từ A vẽ đường kính AQ => tam giác ACQ vuông tại C => \(\widehat{CAO}\)+ \(\widehat{AMC}\)=90 (1)
AK là đg cao => tam giác AKB vuông tại K => \(\widehat{BAK}\)+ \(\widehat{ABK}\)=90 (2)
mà \(\widehat{AMC}\)= \(\widehat{ABK}\)(cùng chắn \(\widebat{AC}\)) (3)
Từ (1),(2),(3) => \(\widehat{CAO}\)= \(\widehat{BAK}\)
mà \(\widehat{BAM}\)= \(\widehat{MAC}\)(cmt)
\(\widehat{BAM}\)= \(\widehat{BAK}\)+ \(\widehat{KAM}\)
\(\widehat{MAC}\)= \(\widehat{CAO}\)+\(\widehat{MAO}\)
=> \(\widehat{KAM}\)= \(\widehat{MAO}\)

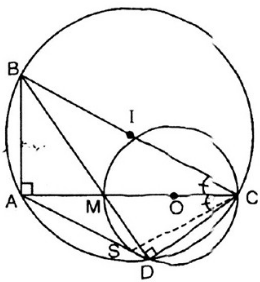
a, ta có ^BAC=900(góc nội tiếp chắn nửa đường tròn đường kính BC)
^MDC=900(góc nội tiếp chắn nửa đường tròn đường kính MC)
=>^BAC=^MDC(=900)
=>tứ giác ABCD nội tiếp (hai đỉnh A và D kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau)
b. vì tứ giác ABCD nội tiếp (câu a) nên ^ABD=^ACD (hai góc nội tiếp cùng chắn cung AD)
c, ta có bốn điểm D,S,C,M cùng thuộc đường tròn đường kính MC
=>tứ giác DSCM nội tiếp
=>^ADM=^SCM (cùng bù với ^MDS)
Mà ADCB nội tiếp nên ^ADM=^MCB( hai góc nội tiếp cùng chắn cung AB)
Do đó ^SCM=^MCB
=>CA là tia phân giác ^SCB

Mình sẽ làm từ câu C nha vì câu C có liên quan đến câu cuối
c/ Xét tam giác ABF và tam giác AEC ta có :
Góc BAF = góc CAE ( AF là phân giác)
góc ABF = góc AEC ( 2 góc nt chắn cung AC)
=>tam giác ABF đồng dạng tam giác AEC (g-g)
=>\(\frac{AB}{AE}=\frac{AF}{AC}\)=>AB.AC=AE.AF
d/ Xét tam giác ABF và tam giác CFE ta có:
góc ABF = góc FEC ( 2 góc nt chắn cung AC )
góc BAF = góc FCE (2 góc nt chắn cung EB )
=> tam giác ABF đồng dạng tam giác CEF (g-g)
=>\(\frac{FB}{FE}=\frac{FA}{FC}\)=>FB.FC=FA.FE
Ta có AF.AE=AB.AC (cmt)
AF.FE=BF.CF (cmt)
=> AF.AE-AF.FE = AB.AC - BF.CF
=> AF(AE-FE) = AB.AC - BF.CF
=> \(AF^2=AB.AC-BF.CF\)

a) Xét (O) có AE là tia phân giác của góc BAC
=> ^BAE=^CAE
=> sđBE=sđCE
=> BE=CE (liên hệ giữa cung và dây cung)
=> tam giác BEC cân tại E (đpcm)
b) Tứ giác ABEC nội tiếp (O)
=> ^BAC+^BEC=180 độ (2 góc đối nhau)
<=> ^BEC=180 độ - ^BAC
Tam giác ABC có ^BAC+^ABC+^BCA=180 độ
=> =180 độ - ^BAC=^ABC+^BCA
Suy ra Góc BEC = góc ABC + góc ACB (đpcm)
c) AE là tia phân giác của góc BAC
=> ^BAE=^CAE
Hay ^BAF=^CAE
Tứ giác ABEC nội tiếp (O)
=> ^ABC=^AEC (2 góc nt chắn cung AC)
Hay ^ABF=^AEC
Xét tam giác ABF và tam giác AEC có:
^ABF=^AEC
^BAF=^CAE
=> tam giác ABF ~ tam giác AEC (g-g)
=> AB/AF=AE/AC
<=> AB.AC=AE.AF (đpcm)