Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

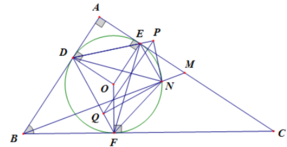
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.

Các bạn ơi, giúp mk vs, mai mk phải đi hc r mà ko có bài

Lời giải:
Ta có:
$PM\parallel AC$ nên $\widehat{PMB}=\widehat{ACB}$
Mà $\widehat{ACB}=\widehat{ABC}=\widehat{PBM}$ do tam giác $ABC$ cân nên $\widehat{PMB}=\widehat{PBM}$
$\Rightarrow \triangle PBM$ cân tại $P$
$\Rightarrow PB=PM$
Mà $PM=PD$ do tính đối xứng
$\Rightarrow PB=PM=PD$ nên $P$ là tâm đường tròn ngoại tiếp $(DBM)$
$\Rightarrow \widehat{BDM}=\frac{1}{2}\widehat{BPM}$ (tính chất góc nt và góc ở tâm cùng chắn 1 cung)
$=\frac{1}{2}\widehat{BAC}$
Tương tự, $Q$ cũng là tâm ngoại tiếp $(DCM)$
$\Rightarrow \widehat{MDC}=\frac{1}{2}\widehat{MQC}=\frac{1}{2}\widehat{BAC}$
Như vậy:
$\widehat{BDC}=\widehat{BDM}+\widehat{MDC}=\widehat{BAC}$
Kéo theo $D\in (ABC)$
Ta có đpcm.

Dễ thấy: MF là đường trung bình của \(\Delta\)PQC => MF // PC => ^FMP = ^APQ (So le trong)
Do PQ là tiếp xúc với đường tròn (MEF) nên ^FMP = ^MEF (Cùng chắn cung MF lớn)
=> ^APQ = ^MEF. Tương tự: ^AQP = ^MFE => \(\Delta\)PAQ ~ \(\Delta\)EMF (g.g) => \(\frac{ME}{AP}=\frac{MF}{AQ}\)
Mà ME = BQ/2; MF = CP/2 => \(\frac{BQ}{AP}=\frac{CP}{AQ}\) (*)
Trên cạnh AB lấy điểm K, trên cạnh AC lấy điểm N sao cho AK=BQ; AN=CP, thế vào (*) => \(\frac{AK}{AP}=\frac{AN}{AQ}\)
=> \(\Delta\)AKP ~ \(\Delta\)ANQ (c.g.c) => ^AKP = ^ANQ => Tứ giác KPNQ nội tiếp
Dễ dàng chứng minh: \(\Delta\)OAK = \(\Delta\)OBQ (c.g.c) => OK=OQ => O nằm trên trung trực KQ
Tương tự: OP=ON => O nằm trên trung trực của PN.
Từ đó: O là giao điểm 2 đường trung trực của KQ,PN. Lại có: Tứ giác KPNQ nội tiếp (cmt)
=> O là tâm đường tròn (KPNQ) => OP=OQ (đpcm).