Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, 3 đường trung tuyến cách nhau tại trọng tâm, khoảng cách từ trọng tâm đến đỉnh bằng \(\dfrac{2}{3}\) độ dài trung tuyến đi qua đỉnh đó
Từ định lí trên ta có \(\left\{{}\begin{matrix}m_a=\dfrac{2}{3}GA\\m_b=\dfrac{2}{3}GB\\m_c=\dfrac{2}{3}GC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m_a^2=\dfrac{4}{9}GA^2\\m_b^2=\dfrac{4}{9}GB^2\\m_c^2=\dfrac{4}{9}GB^2\end{matrix}\right.\)
Đặt D = GA2 + GB2 + GC2
⇒ D = ma2 + mb2 + mc2
⇒ D = \(\dfrac{2\left(a^2+b^2\right)-c^2+2\left(b^2+c^2\right)-a^2+2\left(a^2+c^2\right)-b^2}{4}\)
⇒ D = \(\dfrac{a^2+b^2+c^2}{3}\)
b, cotA = \(\dfrac{cosA}{sinA}=\dfrac{\dfrac{b^2+c^2-a^2}{2bc}}{\dfrac{a}{2R}}=R.\dfrac{b^2+c^2-a^2}{abc}\)
Tương tự ta có
cotB = \(R.\dfrac{a^2+c^2-b^2}{abc}\)
cotC = \(R.\dfrac{a^2+b^2-c^2}{abc}\)
Vậy cotA + cotB + cotC = \(R.\dfrac{a^2+b^2+c^2}{abc}\) (1)
Theo công thức tính diện tích
S = \(\dfrac{abc}{4R}\) ⇒ abc = 4 . S . R
Thế vào (1) ta có
cotA + cotB + cotC = \(R.\dfrac{a^2+b^2+c^2}{4.S.R}=\dfrac{a^2+b^2+c^2}{4S}\)
a, \(\overrightarrow{GA}=-\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(\Rightarrow GA^2=\dfrac{1}{9}\left(AB^2+AC^2+2AB.AC.cosA\right)\)
\(=\dfrac{1}{9}\left(c^2+b^2+2bc.cosA\right)\)
\(=\dfrac{1}{9}\left(c^2+b^2+b^2+c^2-a^2\right)=\dfrac{2b^2+2c^2-a^2}{9}\)
Tương tự \(GB^2=\dfrac{2a^2+2c^2-b^2}{9}\); \(GC^2=\dfrac{2a^2+2b^2-c^2}{9}\)
\(\Rightarrow GA^2+GB^2+GC^2=\dfrac{a^2+b^2+c^2}{3}\)
b, \(cotA+cotB+cotC=\dfrac{cosA}{sinA}+\dfrac{cosB}{sinB}+\dfrac{cosC}{sinC}\)
\(=\dfrac{b^2+c^2-a^2}{2bcsinA}+\dfrac{a^2+c^2-b^2}{2acsinB}+\dfrac{a^2+b^2-c^2}{2absinC}\)
\(=\dfrac{b^2+c^2-a^2}{2bcsinA}+\dfrac{a^2+c^2-b^2}{2ac.\dfrac{b}{a}sinA}+\dfrac{a^2+b^2-c^2}{2ab.\dfrac{c}{a}sinA}\)
\(=\dfrac{a}{2sinA}\left(\dfrac{b^2+c^2-a^2}{abc}+\dfrac{a^2+c^2-b^2}{abc}+\dfrac{a^2+b^2-c^2}{abc}\right)\)
\(=\dfrac{a^2+b^2+c^2}{2bcsinA}=\dfrac{a^2+b^2+c^2}{4.S}\)
Theo tính chất của tam giác, ta có:
\(A+B+C=180^0\)
\(\Rightarrow\dfrac{A+B+C}{2}=90^0\)
\(\Rightarrow\dfrac{B+C}{2}=90^0-\dfrac{A}{2}\)
\(\Rightarrow tan\left(\dfrac{B+C}{2}\right)=tan\left(90^0-\dfrac{A}{2}\right)\)
\(\Rightarrow tan\left(\dfrac{B+C}{2}\right)=cot\left(\dfrac{A}{2}\right)\)
a/ Ta có: \(\left\{{}\begin{matrix}cosB=\frac{a^2+c^2-b^2}{2ac}\\S=\frac{1}{2}ac.sinB\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}cosB=\frac{a^2+c^2-b^2}{2ac}\\sinB=\frac{2S}{ac}\end{matrix}\right.\)
\(\Rightarrow cotB=\frac{cosB}{sinB}=\frac{\left(a^2+c^2-b^2\right).ac}{2ac.2S}=\frac{a^2+c^2-b^2}{4S}\)
b/ Tương tự: \(cotA=\frac{b^2+c^2-a^2}{4S}\) ; \(cotC=\frac{a^2+b^2-c^2}{4S}\)
\(\Rightarrow cotA+cotB+cotC=\frac{a^2+b^2+c^2}{4S}\)
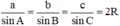(Định lý Sin)
