Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có \(\widehat{AEH}=90\)
\(\widehat{AFH}\)=90
\(\widehat{AEH}+\widehat{AFH}=90+90=180\) tổng 2 góc đối nhau
⇒ tứ giác AEHF là tứ giác nội tiếp

a: Xét (O) có
AB là tiếp tuyến có B là tiếp điểm
AC là tiếp tuyến có C là tiếp điểm
Do đó: AB=AC
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(1)
ta có: BA=AC
nên A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA⊥BC

Ta có
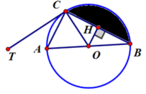
T C A ^ = A B C ^ = 30 0 . cos A C B ^ = B C A B = 3 2 ⇒ B C = 3 c m .
Kẻ đường cao OH trong tam giác OBC. Ta có sin O B H ^ = O H O B = 1 2 ⇒ O H = 1 2 c m .
Diện tích tam giác OBC là s 1 = 1 2 . O H . B C = 3 4 c m 2 .
Ta có B O C ^ = 120 0 (vì O B C ^ = B C O ^ = 30 0 ).
Diện tích hình quạt chứa phần tô đen là s 2 = 120 360 . π . R 2 = π 3 c m 2 .
Diện tích phần tô đen là s = s 2 − s 1 = π 3 − 3 4 c m 2 .

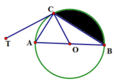
Gọi tiếp điểm giữa đường tròn nội tiếp \(\Delta\)ABC với BC,CA,AB lần lượt là D,E,F; BM cắt đường tròn này tại U,V.
Đặt \(BC=m;CA=n;BU=UV=VM=p;AE=AF=q\left(m,n,p,q>0;q< x\right)\)
Áp dụng phương tích đường tròn ta có: \(BF^2=ME^2=2p^2\Rightarrow AB=AM=\frac{n}{2}\)hay \(n=2x\)
Đồng thời \(CD=CE=2x-q;BD=BF=x-q\Rightarrow m=3x-2q;p^2=\frac{\left(x-q\right)^2}{2}\)
Từ đó; áp dụng công thức đường trung tuyến, ta có:
\(\frac{9}{2}\left(x-q\right)^2=\frac{x^2+\left(3x-2q\right)^2}{2}-x^2\Leftrightarrow x^2-6xq+5q^2=0\Leftrightarrow\orbr{\begin{cases}q=x\left(l\right)\\q=\frac{x}{5}\end{cases}}\)
Do vậy \(m=3x-\frac{2}{5}x=\frac{13}{5}x\)
Áp dụng công thức Heron vào \(\Delta\)ABC, ta thu được: \(S_{ABC}=\sqrt{x^4.\frac{14}{5}.\frac{9}{5}.\frac{4}{5}.\frac{1}{5}}=\frac{6\sqrt{14}}{25}x^2.\)