Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là giao điểm của BM và CN. Ta có:
Diện tích tam giác ABC = 1/2 * AB * AC = 1/2 * 8 cm * 12 cm = 48 cm^2
Theo định lí Menelaus, ta có:
(BH/HA) * (AN/NC) * (CM/MB) = 1
Thay giá trị vào ta được:
(BH/HA) * (4/8) * (5/7) = 1
Suy ra: BH/HA = 14/15
Do đó, AH = AB - BH = 8 cm - (14/15)*8 cm = 8/15 cm
Tương tự, ta có: CH = 12/15 cm
Áp dụng công thức diện tích tam giác bằng nửa tích chất của đường cao, ta có:
Diện tích tam giác AMN = 1/2 * AM * NH = 1/2 * (AB - BM) * AH = 1/2 * (8 cm - 5 cm) * 8/15 cm = 8/15 cm^2
Vậy diện tích hình tam giác AMN là 8/15 cm^2.

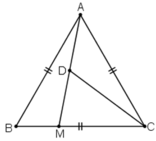
a) Do tam giác ABC là tam giác đều nên 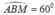 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
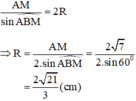
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
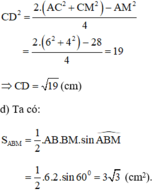
\(AM=AB+BM=13\left(cm\right)\)
\(AN=AC+CN=16\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AB.AC.sinA\Rightarrow sinA=\dfrac{2S_{ABC}}{AB.AC}=\dfrac{3}{4}\)
\(\Rightarrow S_{AMN}=\dfrac{1}{2}AM.AN.sinA=\dfrac{1}{2}.13.16.\dfrac{3}{4}=...\)