K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
\(AM=AB+BM=13\left(cm\right)\)
\(AN=AC+CN=16\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AB.AC.sinA\Rightarrow sinA=\dfrac{2S_{ABC}}{AB.AC}=\dfrac{3}{4}\)
\(\Rightarrow S_{AMN}=\dfrac{1}{2}AM.AN.sinA=\dfrac{1}{2}.13.16.\dfrac{3}{4}=...\)

CM
28 tháng 2 2018
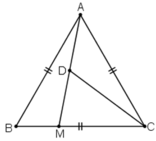
a) Do tam giác ABC là tam giác đều nên 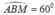 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
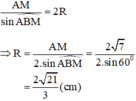
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
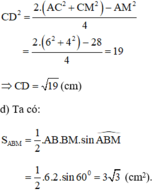
Gọi H là giao điểm của BM và CN. Ta có:
Diện tích tam giác ABC = 1/2 * AB * AC = 1/2 * 8 cm * 12 cm = 48 cm^2
Theo định lí Menelaus, ta có:
(BH/HA) * (AN/NC) * (CM/MB) = 1
Thay giá trị vào ta được:
(BH/HA) * (4/8) * (5/7) = 1
Suy ra: BH/HA = 14/15
Do đó, AH = AB - BH = 8 cm - (14/15)*8 cm = 8/15 cm
Tương tự, ta có: CH = 12/15 cm
Áp dụng công thức diện tích tam giác bằng nửa tích chất của đường cao, ta có:
Diện tích tam giác AMN = 1/2 * AM * NH = 1/2 * (AB - BM) * AH = 1/2 * (8 cm - 5 cm) * 8/15 cm = 8/15 cm^2
Vậy diện tích hình tam giác AMN là 8/15 cm^2.