Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S 1 , S 2 , S 3 . Ta có:
S = S 1 + S 2 + S 3
Trong đó: S = 1/2 AD.BC = 1/2 BE. AC = 1/2 CF. AB
S 1 = 1/2 MT. AB
S 2 = 1/2 MK. AC
S 3 = 1/2 MH. BC
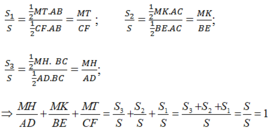

a) Ta có: AM//BD
=> \(\dfrac{AM}{BD}=\dfrac{AF}{FB}\)
Xét tam giác ACB có CF là đường phân giác góc C
=> \(\dfrac{AC}{BC}=\dfrac{AF}{BF}\) (theo t/chất đường phân giác trong tam giác)
=> \(\dfrac{AM}{BD}=\dfrac{AC}{BC}\)


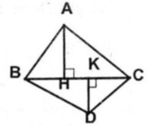
Gọi K là giao điểm của 3 đg pg trong tg ABC
Do AD ,BE ,CF lần lượt là các đg pg của tg ABC nên ta có:
\(\frac{BD}{DC}=\frac{AB}{AC}\) => AB.DC=AC.BD ; (*)
\(\frac{AE}{EC}=\frac{AB}{AC}\) ; (1)
\(\frac{AF}{BF}=\frac{AC}{BC}\) ;(2)
Mặt khá: MN//BC (gt) => tg ANE\(\infty\)tg CDE (Ta-lét) =>\(\frac{AN}{DC}=\frac{AE}{EC}\) (3)
và tg AMF \(\infty\)tg BDF (Ta-lét) => \(\frac{AM}{BD}=\frac{AF}{BF}\) (4)
Từ (1),(3)=>\(\frac{AN}{DC}=\frac{AB}{BC}=>AN.BC=AB.DC\) (**)
Từ (2),(4)=> \(\frac{AM}{BD}=\frac{AC}{BC}=>AM.BC=AC.DB\) (***)
Từ (*),(**),(***)=> AN.BC=AM.BC=> AM=AN . Mà M,A,N thẳng hàng nên A là t/đ của MN (đpcm)