Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé!
a) Ta có: AB là trung trực của ME => AE=AM (1)
Tương tự AC cũng là trung trự của MF => AF=AM (2)
(1)(2) => AE=AF
Chứng tỏ trung trực của EF đi qua A
b) Ta có: BE=BM (AB là trung trực của EM)
Tương tự CF=CM mà BM+MC=BC
=> BE+CF=BC

a, Ta thấy AB là là trung trực của EH nên AE= AH
tương trự AC là trung trực của HF nên AF=AH
Xét tam giác AEF có AF=AE
vậy tram giác AEF cân tại A
b, Ta thấy BA là trung trực EH nên AEH=AHE
IEH=IHE
suy ra AEI =AHI
Tương tự ta suy ra được được AHK=AFK
mà AFK=AEI nên AHI=AHK
vậy HA là tia phân giác của IHK

a) Ta có: AB là đường trung trực của EM(gt)
⇒A nằm trên đường trung trực của EM
hay AE=AM(tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AC là đường trung trực của MF(gt)
⇒A nằm trên đường trung trực của FM
hay AM=AF(tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AE=AF
hay A nằm trên đường trung trực của EF(tính chất đường trung trực của một đoạn thẳng)
b) Ta có: AB là đường trung trực của EM(gt)
⇒B nằm trên đường trung trực của EM
hay BE=BM(tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: AC là đường trung trực của MF(gt)
⇒C nằm trên đường trung trực của FM
hay CM=CF(tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: BM+CM=BC(M nằm giữa B và C)(5)
Từ (3), (4) và (5) suy ra BC=BE+CF(đpcm)
c) Xét ΔABE và ΔABM có
AE=AM(cmt)
AB là cạnh chung
BE=BM(cmt)
Do đó: ΔABE=ΔABM(c-c-c)
⇒\(\widehat{EAB}=\widehat{BAM}\)(hai góc tương ứng)
mà tia AB nằm giữa hai tia AE,AM
nên AB là tia phân giác của \(\widehat{EAM}\)
hay \(\widehat{EAM}=2\cdot\widehat{BAM}\)(6)
Xét ΔAMC và ΔAFC có
AM=AF(cmt)
AC chung
MC=CF(cmt)
Do đó: ΔAMC=ΔAFC(c-c-c)
⇒\(\widehat{MAC}=\widehat{FAC}\)(hai góc tương ứng)
mà tia AC nằm giữa hai tia AF,AM
nên AC là tia phân giác của \(\widehat{FAM}\)
hay \(\widehat{FAM}=2\cdot\widehat{CAM}\)(7)
Ta có: \(\widehat{BAM}+\widehat{CAM}=\widehat{BAC}\)(tia AM nằm giữa hai tia AB,AC)
hay \(\widehat{BAM}+\widehat{CAM}=60^0\)(8)
Ta có: \(2\cdot\widehat{BAM}+2\cdot\widehat{CAM}=\widehat{EAM}+\widehat{FAM}\)
hay \(2\cdot\left(\widehat{BAM}+\widehat{CAM}\right)=\widehat{EAM}+\widehat{FAM}\)(9)
Từ (6),(7),(8) và (9) suy ra:
\(\widehat{EAM}+\widehat{FAM}=120^0\)(10)
Ta có: \(\widehat{EAM}+\widehat{FAM}=\widehat{FAE}\)(tia AM nằm giữa hai tia AE,AF)(11)
Từ (10) và (11) suy ra: \(\widehat{FAE}=120^0\)
Xét ΔAEF có AE=AF(cmt)
nên ΔAEF cân tại A(định nghĩa tam giác cân)
⇒\(\widehat{AEF}=\widehat{AFE}=\frac{180^0-\widehat{EAF}}{2}\)(số đo của các góc ở đáy trong ΔAEF)
hay \(\widehat{AEF}=30^0\); \(\widehat{AFE}=30^0\)
Vậy: \(\widehat{FAE}=120^0\); \(\widehat{AEF}=30^0\); \(\widehat{AFE}=30^0\)

a, Ax là phân giác của góc BAC (gt)
K thuộc Ax
KE _|_ AB (gt); KF _|_ AC (gt)
=> KE = KF (định lí) (1)
K thuộc đường trung trực của BC (gt)
=> KB = KC (Định lí)
xét tam giác EKB và tam giác FKC có : góc BEK = góc KFC = 90
=> tam giác EKB = tam giác FKC (ch-cgv)
=> BE = CF (đn)
a ) Ta có Ax là đường trung trực của tam giác ABC => Ax là đường trung trực của tam giác ABC
Xét tam giác BEK vuông tại E và tam giác CFK vuông tại F ta có :
BK = KC ( cmt )
BKE = CKF ( đối đỉnh )
=> Tam giác BEK = tam giác CFK
=> BE = CF ( 2 cạnh tương ứng )
mik chỉ làm đc câu a thoi maf hình như đề bị sai á

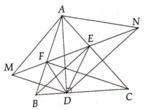


d) A là trung điểm của EF khi 3 điểm E,A,F thẳng hàng và AE=AI
Do đó: \(\widehat{BAC}=90^o\)
Nhận xét: Trường hợp tam giác đã cho có 1 góc tù các đường trung trực của 2 cạnh cắt nhau tại 1 điểm ta cũng có bài toán kết luận tương tự
Nguồn: Hải Ah
Giúp mình vâu abc lun đi bạn