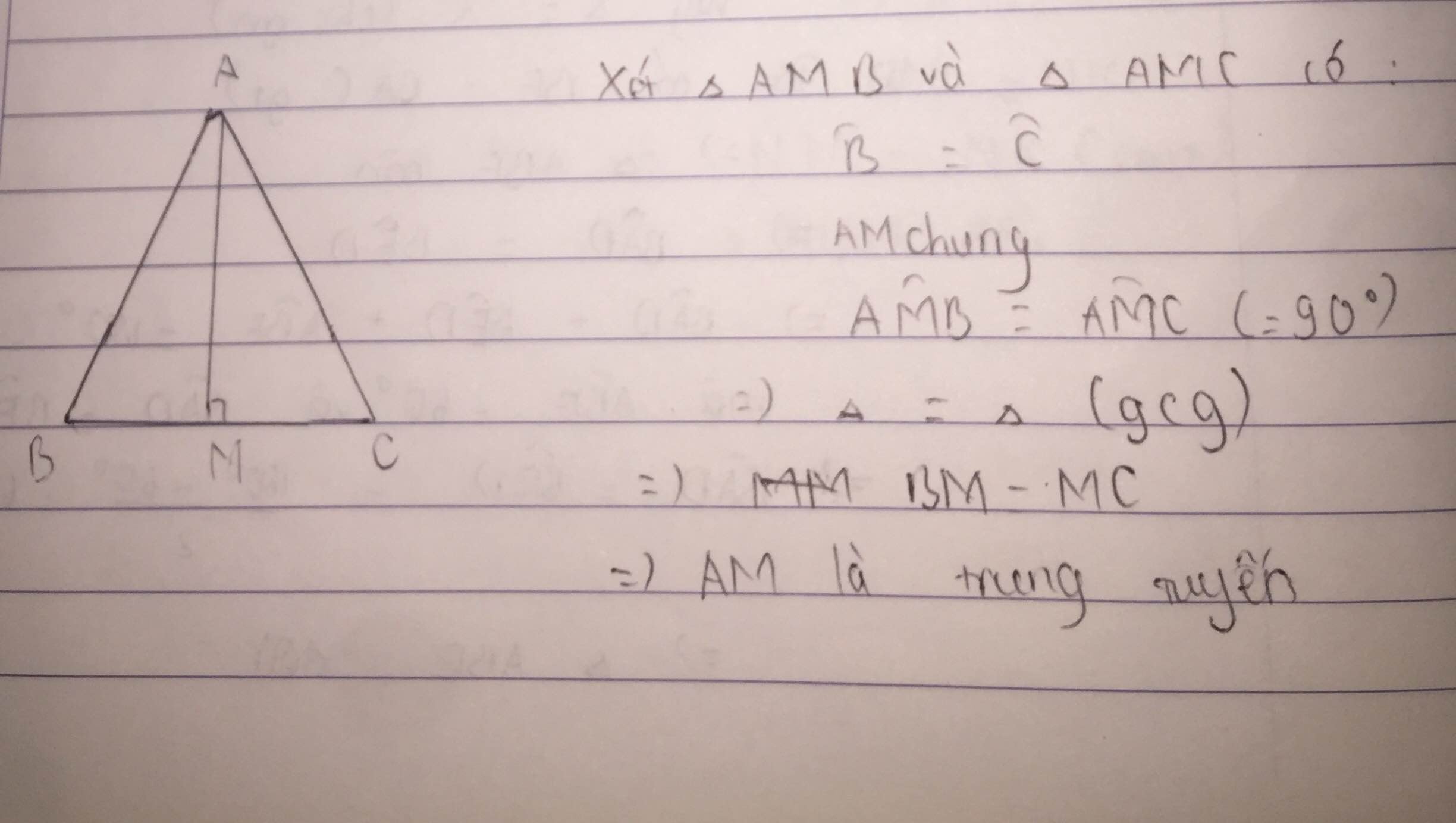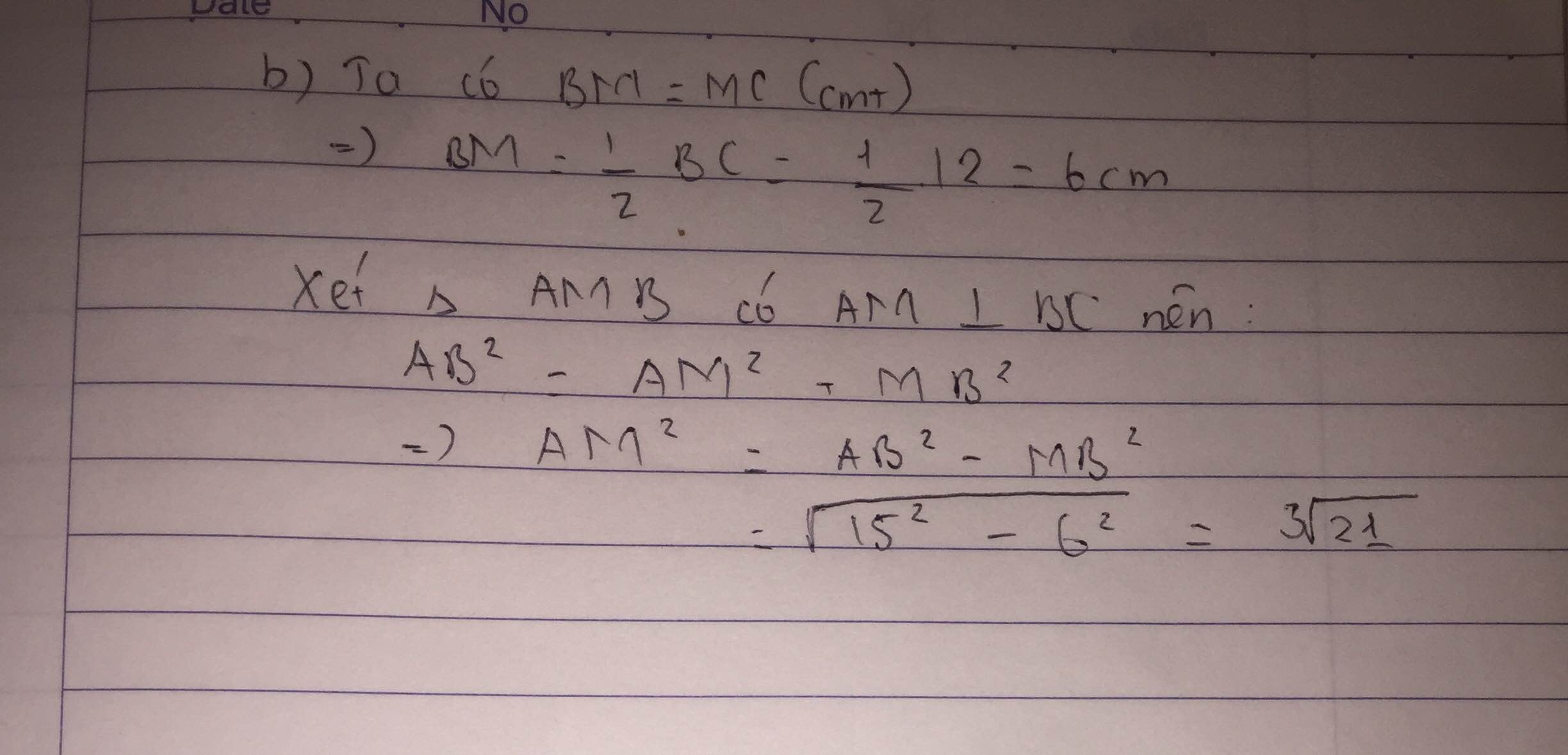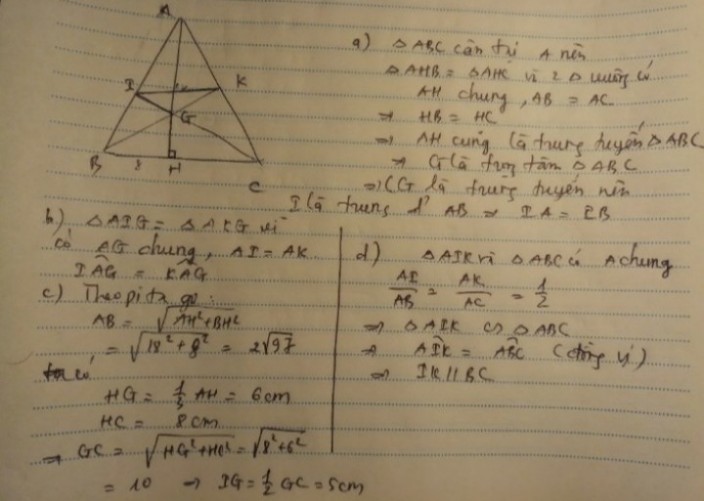Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

refer
a) Vì AH là đường trung tuyến của tam giác ABC cân tại A:
nên HB=HC
Xét tam giác AHB và tam giác AHC:
có:+AB=AC( tam giác ABC cân tại A)
+HB=HC(cmt)
+AH: cạnh chung
Vậy tam giác AHB=tam giác AHC(c.c.c)
b) Vì tam giác AHB=tam giác AHC(cmt)
nên: góc AHB=góc AHC=90 độ( 2 góc tương ứng )
c) HB=HC=BC2=102=5cmHB=HC=BC2=102=5cm
Áp dụng định lí Pytago vào tam giác ABH vuông tại H:
có: AB2=AH2+BI2AB2=AH2+BI2
hay:132=AH2+52132=AH2+52
⇒AH2=132−52⇒AH2=132−52
⇔AH=√132−52=12⇔AH=132−52=12
Vậy AH=12cm
a, Xét Δ AHB và Δ AHC, có :
AH là cạnh chung
AB = AC (Δ ABC cân tại A)
HB = HC (AH là đường trung tuyến của BC)
=> Δ AHB = Δ AHC (c.c.c)
b, Xét Δ ABC cân tại A, có :
AH là đường trung tuyến
=> AH là đường cao
=> \(\widehat{AHC}=\widehat{AHB}=90^o\)
c, đề kì dzậy

Để tớ làm lại cho. Nguyên phần tính BG luôn, cái kia out :))
Ta có tam giác ABC cân tại A => AD vừa là phân giác vừa là đường cao => AD vuông góc BC tại D (bổ sung kí hiệu vô nhé)
Ta có: D là trung điểm BC => BD = CD = BC : 2 = 6 : 2 = 3 (cm)
Xét tam giác ABD vuông tại D có:
\(AD^2+BD^2=AB^2\left(pytago\right)\)
\(AD^2+3^2=5^2\)
\(AD^2=5^2-3^2=25-9=16\)
\(\Rightarrow AD=\sqrt{16}=4\left(cm\right)\)
Vì G là trọng tâm tam giác ABC => \(GD=\frac{1}{3}AD\Leftrightarrow GD=\frac{1}{3}.4=\frac{4}{3}\left(cm\right)\)
Xét tam giác BGD vuông tại D có:
\(GD^2+BD^2=BG^2\left(pytago\right)\)
\(\left(\frac{4}{3}\right)^2+3^2=BG^2\)
\(\frac{97}{9}=BG^2\Leftrightarrow BG=\sqrt{\frac{97}{9}}\approx3,3\left(cm\right)\)
a/ Ta có tam giác ABC cân tại A => AD vừa là đường phân giác vừa là trung tuyến => BD = CD
Xét tam giác ABC có 2 đường trung tuyến AD;BE cắt nhau tại G
=> G là trọng tâm của tam giác ABC
=> CF là đường trung tuyến thứ 3
=> F là trung điểm AB hay FB = FA
b/ Vì tam giác ABC cân tại A => AB = AC = 5 cm
Ta có: \(AE=EC=\frac{AC}{2}=\frac{5}{2}=2,5\left(cm\right)\)(Vì E là trung điểm AC)
Xét tam giác BEC vuông tại E có:
\(BE^2+EC^2=BC^2\left(pytago\right)\)
\(BE^2+2,5^2=6^2\)
\(BE^2=6^2-2,5^2=29,75\)
\(\Rightarrow BE=\sqrt{29,75}\approx5,5\left(cm\right)\)
Vì G là trọng tâm tam giác ABC (cmt)
\(\Rightarrow BG=\frac{2}{3}BE=\frac{2}{3}.5,5\approx3,7\left(cm\right)\)

Vì G là trọng tâm ΔABC
⇒AG=2323 AH=2323 18=12(cm)
Mà AG=2GH
⇒GH=AG2AG2 =122122 =6(cm)
BH=HC(do AH là trung tuyến BC)
⇒BH=HC=BC2BC2 =162162 =8(cm)
Xét ΔGHC có:
GH²+HC²=GC²(Định lí Pi-ta-go)
⇒6²+8²=GC²
⇒36+64=GC²
⇒GC²=100=10²
⇒GC=10(cm)
Mà GC=2GI
⇒GI=GC2GC2 =102102=5(cm)
Vậy độ dài cạnh GI là 5cm
d)Ta có:
Theo b) GI=GK
⇒ΔIGK là tam giác cân tại G
{GC=2GIGB=2GK{GC=2GIGB=2GK
Mà GI=GK
⇒GC=GB
⇒ΔGBC là tam giác cân tại G
Ta có:
∠KIG=∠IKG=180∗−∠IGK2180∗−∠IGK2
∠GBC=∠GCB=180∗−∠BGC2180∗−∠BGC2
Mà ∠IGK=∠BGC(đối đỉnh)
⇒∠KIG=∠GCB
Mà 2 góc ở vị trí so le trong
⇒IK=BC