Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

DA*DP=DB*DC
=>DA/DC=DB/DP
=>ΔDAB đồng dạng với ΔDCP
=>góc BAD=góc PCD
=>ABPC nội tiếp

y'
a) b) Đưa các đẳng thức về dạng đẳng thức của các tỉ số và áp dụng để chứng minh các cặp tam giác đồng dạng.
c) Từ hai phần a và b, ta suy ra
a) b) Đưa các đẳng thức về dạng đẳng thức của các tỉ số và áp dụng để chứng minh các cặp tam giác đồng dạng.
c) Từ hai phần a và b, ta suy ra .

Lời giải:
a)
Vì $AB,AC$ là tiếp tuyến $(O)$ nên:
$AB\perp BO; AC\perp CO$
$\Rightarrow \widehat{ABO}=\widehat{ACO}=90^0$
$\Rightarrow \widehat{ABO}+\widehat{ACO}=180^0$
Tứ giác $ABOC$ có tổng 2 góc đối bằng $180^0$ nên là tgnt (đpcm)
b)
Xét tam giác $ABE$ và $AFB$ có:
$\widehat{A}$ chung
$\widehat{ABE}=\widehat{AFB}$ (góc tạo bởi tiếp tuyến và dây cung thì bằng góc nt chắn cung đó)
$\Rightarrow \triangle ABE\sim \triangle AFB$ (g.g)
$\Rightarrow \frac{BE}{BF}=\frac{AE}{AB}(1)$
Tương tự:
$\triangle ACE\sim \triangle AFC$ (g.g)
$\Rightarrow \frac{CE}{CF}=\frac{AE}{AC}(2)$
Từ $(1);(2)$ kết hợp với $AB=AC$ (tính chất 2 tiếp tuyến giao nhau) nên $\frac{BE}{BF}=\frac{CE}{CF}$
$\Rightarrow BE.CF=BF.CE$ (đpcm)

a: Xét tứ giác ABCD có
\(\widehat{BAC}=\widehat{BDC}=90^0\)
Do đó: ABCD là tứ giác nội tiếp

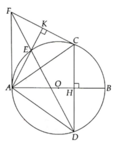
a, Học sinh tự chứng minh
b, DADB vuông tại D, có đường cao DH Þ A D 2 = AH.AB
c, E A C ^ = E D C ^ = 1 2 s đ E C ⏜ ; E A C ^ = K H C ^ (Tứ giác AKCH nội tiếp)
=> E D C ^ = K H C ^ => DF//HK (H là trung điểm DC nên K là trung điểm FC) => Đpcm